
【題目】如果一個點是一個指數函數和一個對數函數的圖像的交點,那么稱這個點為"好點".下列四個點P1(1,1),P2(1,2),P3(![]() ,
,![]() ),P4(2,2)中,"好點"有( )個
),P4(2,2)中,"好點"有( )個
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
可設指數函數為y=ax,對數函數為y=logbx,容易判斷P1,P2不在對數函數圖象上,從而判斷這兩點不是“好點”,然后將P3的坐標分別代入指數函數和對數函數解析式,從而可解出a,b,進而判斷出P3為“好點”,同樣的方法可判斷P4為好點,進而找出正確選項.
設指數函數為y=ax,對數函數為y=logbx;
對于對數函數,x=1時,y=0,則P1,P2不是對數函數圖象上的點;
∴P1,P2不是好點;
將P3的坐標分別代入指數函數和對數函數解析式得:
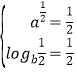 ;
;
解得![]() ;
;
即P3是指數函數![]() 和對數函數
和對數函數![]() 的交點,即P3為“好點”;
的交點,即P3為“好點”;
同樣,將P4坐標代入函數解析式得:
![]() ;
;
解得![]() ;
;
∴P4是“好點”;
∴“好點”個數為2.
故選:B.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】學校計劃利用周五下午第一、二、三節課舉辦語文、數學、英語、理綜4科的專題講座,每科一節課,每節至少有一科,且數學、理綜不安排在同一節,則不同的安排方法共有( )
A. 6種 B. 24種 C. 30種 D. 36種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓的中心在原點,焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,且經過點
,且經過點![]() ,直線
,直線![]() 交橢圓于不同的兩點
交橢圓于不同的兩點![]() .
.
(1)求橢圓的方程;
(2)求![]() 的取值范圍;
的取值范圍;
(3)若直線![]() 不過點
不過點![]() ,求證:直線
,求證:直線![]() 的斜率互為相反數.
的斜率互為相反數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以直角坐標系的原點為極點,以
為參數),以直角坐標系的原點為極點,以![]() 軸的正半軸為極軸建立極坐標系,已知直線
軸的正半軸為極軸建立極坐標系,已知直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程;
的普通方程;
(2)若![]() 與曲線
與曲線![]() 相切,且
相切,且![]() 與坐標軸交于
與坐標軸交于![]() 兩點,求以
兩點,求以![]() 為直徑的圓的極坐標方程.
為直徑的圓的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型商場去年國慶期間累計生成![]() 萬張購物單,從中隨機抽出
萬張購物單,從中隨機抽出![]() 張,對每單消費金額進行統計得到下表:
張,對每單消費金額進行統計得到下表:
消費金額(單位:元) |
|
|
|
|
|
購物單張數 | 25 | 25 | 30 |
由于工作人員失誤,后兩欄數據無法辨識,但當時記錄表明,根據由以上數據繪制成的頻率分布直方圖所估計出的每單消費額的中位數與平均數恰好相等.用頻率估計概率,完成下列問題:
(1)估計去年國慶期間該商場累計生成的購物單中,單筆消費額超過![]() 元的概率;
元的概率;
(2)為鼓勵顧客消費,該商場計劃在今年國慶期間進行促銷活動,凡單筆消費超過![]() 元者,可抽獎一次.抽獎規則為:從裝有大小材質完全相同的
元者,可抽獎一次.抽獎規則為:從裝有大小材質完全相同的![]() 個紅球和
個紅球和![]() 個黑球的不透明口袋中,隨機摸出
個黑球的不透明口袋中,隨機摸出![]() 個小球,并記錄兩種顏色小球的數量差的絕對值
個小球,并記錄兩種顏色小球的數量差的絕對值![]() ,當
,當![]() 時,消費者可分別獲得價值
時,消費者可分別獲得價值![]() 元、
元、![]() 元和
元和![]() 元的購物券.求參與抽獎的消費者獲得購物券的價值的數學期望.
元的購物券.求參與抽獎的消費者獲得購物券的價值的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校或班級舉行活動,通常需要張貼海報進行宣傳.現讓你設計一張如圖所示的豎向張貼的海報,要求版心面積為128 dm2,上、下兩邊各空2 dm,左、右兩邊各空1 dm.如何設計海報的尺寸,才能使四周空白面積最小?
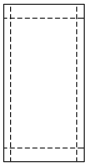
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 中點.將
中點.將![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如圖2).
(如圖2).

(1)求證:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出
? 若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com