②③④
分析:①△PF
1F
2面積S=

|F
1F
2|•|y|,所以當|y|取最大值時,△PF
1F
2面積最大,此時點P為橢圓短軸端點;
②利用橢圓的第一定義,即可求得;
③分斜率存在與不存在討論,假設直線方程代入橢圓方程,借助于韋達定理與橢圓的第二定義,化簡即可;
④根據定點
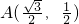
在橢圓

的內部,點P(x,y)為橢圓

上一點,可得
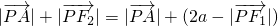
=
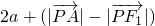
,從而當且僅當P、A、F
1三點共線時,
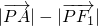
取得最小與最大,
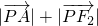
取得最小與最大.
解答:①△PF
1F
2面積S=

|F
1F
2|•|y|=

|y|,所以當|y|取最大值時,△PF
1F
2面積最大,所以點P為橢圓短軸端點時,|y|取最大值,此時y=±1,即△PF
1F
2面積的最大值S=

,故①錯誤;
②∵P,Q在橢圓上,F
1、F
2為橢圓左、右焦點
∴△PF
1Q的周長為2a+2a=4a,
∵a=2
∴△PF
1Q的周長為8,
故②正確;
③斜率存在時,設P(x
1,y
1),Q(x
2,y
2),直線方程為:y=k(x

)
代入橢圓方程

得:
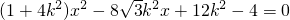
∴
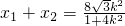
,
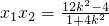
根據橢圓的第二定義可得:
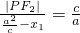
,
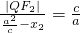
∴|PF
2|=a-ex
1,|QF
2|=a-ex
2∴
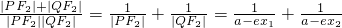
=
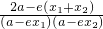
=
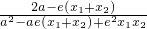
∵
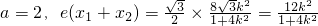
,
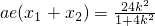
,
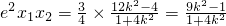
∴
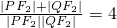
當斜率不存在時,
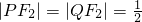
,∴
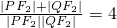
,故③正確;
④∵定點
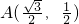
在橢圓

的內部,點P(x,y)為橢圓

上一點,
∴
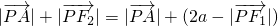
=
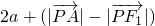
當且僅當P、A、F
1三點共線時,
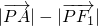
取得最小與最大,
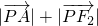
取得最小與最大.
∵
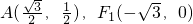
∴
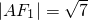
∴
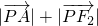
的取值范圍為
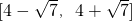
,故④正確
故答案為:②③④
點評:本題以橢圓為載體,考查橢圓的性質,考查橢圓的兩個定義,解題思維有點困難,計算要細心.

 上一點,F1、F2為橢圓左、右焦點,下列結論中:①△PF1F2面積的最大值為
上一點,F1、F2為橢圓左、右焦點,下列結論中:①△PF1F2面積的最大值為 ;②若過點P、F2的直線l與橢圓的另一交點為Q,則△PF1Q的周長為8;③若過點P、F2的直線l與橢圓的另一交點為Q,則恒有
;②若過點P、F2的直線l與橢圓的另一交點為Q,則△PF1Q的周長為8;③若過點P、F2的直線l與橢圓的另一交點為Q,則恒有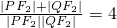 ;對定點
;對定點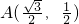 ,則
,則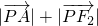 的取值范圍為
的取值范圍為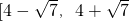 .其中正確結論的番號是________.
.其中正確結論的番號是________. |F1F2|•|y|,所以當|y|取最大值時,△PF1F2面積最大,此時點P為橢圓短軸端點;
|F1F2|•|y|,所以當|y|取最大值時,△PF1F2面積最大,此時點P為橢圓短軸端點;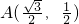 在橢圓
在橢圓 的內部,點P(x,y)為橢圓
的內部,點P(x,y)為橢圓 上一點,可得
上一點,可得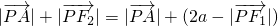 =
=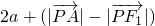 ,從而當且僅當P、A、F1三點共線時,
,從而當且僅當P、A、F1三點共線時,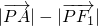 取得最小與最大,
取得最小與最大,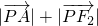 取得最小與最大.
取得最小與最大. |F1F2|•|y|=
|F1F2|•|y|= |y|,所以當|y|取最大值時,△PF1F2面積最大,所以點P為橢圓短軸端點時,|y|取最大值,此時y=±1,即△PF1F2面積的最大值S=
|y|,所以當|y|取最大值時,△PF1F2面積最大,所以點P為橢圓短軸端點時,|y|取最大值,此時y=±1,即△PF1F2面積的最大值S= ,故①錯誤;
,故①錯誤; )
) 得:
得: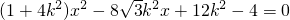
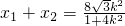 ,
,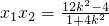
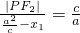 ,
,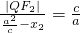
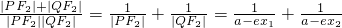
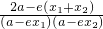 =
=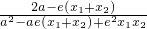
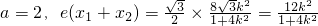 ,
,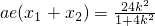 ,
,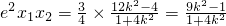
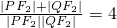
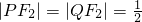 ,∴
,∴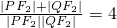 ,故③正確;
,故③正確;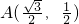 在橢圓
在橢圓 的內部,點P(x,y)為橢圓
的內部,點P(x,y)為橢圓 上一點,
上一點,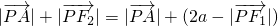 =
=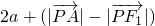
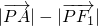 取得最小與最大,
取得最小與最大,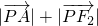 取得最小與最大.
取得最小與最大.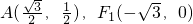
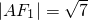
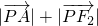 的取值范圍為
的取值范圍為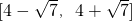 ,故④正確
,故④正確
