
【題目】已知函數f(x)=x﹣1+ ![]() (a∈R).
(a∈R).
(1)若曲線y=f(x)在點(1,f(1))處的切線平行于x軸,求a的值;
(2)求函數f(x)的極值;
(3)當a=1時,若直線l:y=kx﹣1與曲線y=f(x)沒有公共點,求k的最大值.
【答案】
(1)解:由 ![]() ,得f′(x)=1﹣
,得f′(x)=1﹣ ![]() ,
,
∴f′(1)=1﹣ ![]() ,
,
由曲線y=f(x)在點(1,f(1))處的切線平行于x軸,得 ![]() ,即a=e
,即a=e
(2)解:由f′(x)=1﹣ ![]() ,知
,知
若a≤0,則f′(x)>0,函數f(x)在實數集內為增函數,無極值;
若a>0,由f′(x)=1﹣ ![]() =0,得x=lna,
=0,得x=lna,
當x∈(﹣∞,lna)時,f′(x)<0,當x∈(lna,+∞)時,f′(x)>0.
∴f(x)在(﹣∞,lna)上單調遞減,在(lna,+∞)上單調遞增
(3)解:當a=1時,f(x)=x﹣1+ ![]() ,令g(x)=f(x)﹣(kx﹣1)=(1﹣k)x+
,令g(x)=f(x)﹣(kx﹣1)=(1﹣k)x+ ![]() ,
,
則直線l:y=kx﹣1與曲線y=f(x)沒有公共點,
等價于方程g(x)=0在R上沒有實數解.
假設k>1,此時g(0)=1>0,g( ![]() )=﹣1+
)=﹣1+ ![]() <0,
<0,
又函數g(x)的圖象連續不斷,由零點存在定理可知g(x)=0在R上至少有一解,
與“方程g(x)=0在R上沒有實數解”矛盾,故k≤1.
又k=1時,g(x)= ![]() >0,知方程g(x)=0在R上沒有實數解.
>0,知方程g(x)=0在R上沒有實數解.
∴k的最大值為1
【解析】(1)求出原函數的導函數,依題意f′(1)=0,從而可求得a的值;(2)f′(x)=1﹣ ![]() ,分①a≤0時②a>0討論,可知f(x)在∈(﹣∞,lna)上單調遞減,在(lna,+∞)上單調遞增,從而可求其極值;(3)令g(x)=f(x)﹣(kx﹣1)=(1﹣k)x+
,分①a≤0時②a>0討論,可知f(x)在∈(﹣∞,lna)上單調遞減,在(lna,+∞)上單調遞增,從而可求其極值;(3)令g(x)=f(x)﹣(kx﹣1)=(1﹣k)x+ ![]() ,則直線l:y=kx﹣1與曲線y=f(x)沒有公共點,等價于方程g(x)=0在R上沒有實數解,分k>1與k≤1討論即可得答案.
,則直線l:y=kx﹣1與曲線y=f(x)沒有公共點,等價于方程g(x)=0在R上沒有實數解,分k>1與k≤1討論即可得答案.
【考點精析】本題主要考查了利用導數研究函數的單調性的相關知識點,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減才能正確解答此題.
在這個區間單調遞減才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】某校為了探索一種新的教學模式,進行了一項課題實驗,甲班為實驗班,乙班為對比班,甲乙兩班的人數均為50人,一年后對兩班進行測試,測試成績的分組區間為![]() 80,90
80,90![]() 、
、![]() 90,100
90,100![]() 、
、![]() 100,110
100,110![]() 、
、![]() 110,120
110,120![]() 、
、![]() 120,130
120,130![]() ,由此得到兩個班測試成績的頻率分布直方圖:
,由此得到兩個班測試成績的頻率分布直方圖:
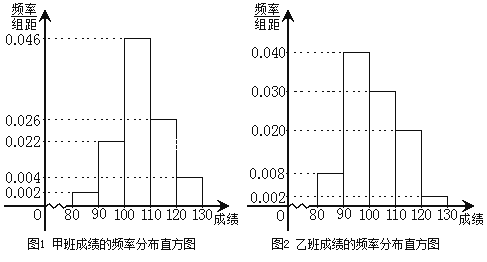
(1)完成下面2×2列聯表,你能有97.5![]() 的把握認為“這兩個班在這次測試中成績的差異與實施課題實驗有關”嗎?并說明理由;
的把握認為“這兩個班在這次測試中成績的差異與實施課題實驗有關”嗎?并說明理由;
成績小于100分 | 成績不小于100分 | 合計 | |
甲班 |
|
| 50 |
乙班 |
|
| 50 |
合計 |
|
| 100 |
(2)根據所給數據可估計在這次測試中,甲班的平均分是105.8,請你估計乙班的平均分,并計算兩班平均分相差幾分?
附:
![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分13分)為了解某校今年高一年級女生的身體素質狀況,從該校高一年級女生中抽取了一部分學生進行“擲鉛球”的項目測試,成績低于5米為不合格,成績在5至7米(含5米不含7米)的為及格,成績在7米至11米(含7米和11米,假定該校高一女生擲鉛球均不超過11米)為優秀.把獲得的所有數據,分成![]() 五組,畫出的頻率分布直方圖如圖所示.已知有4名學生的成績在9米到11米之間.
五組,畫出的頻率分布直方圖如圖所示.已知有4名學生的成績在9米到11米之間.

(1)求實數![]() 的值及參加“擲鉛球”項目測試的人數;
的值及參加“擲鉛球”項目測試的人數;
(2)若從此次測試成績最好和最差的兩組中隨機抽取2名學生再進行其它項目的測試,求所抽取的2名學生自不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在冬季,由于受到低溫和霜凍的影響,蔬菜的價格會隨著需求量的增加而提升.已知某供應商向飯店定期供應某種蔬菜,其價格會隨著日需求量的增加而上升,具體情形統計如下表所示:

(1)根據上表中的數據進行判斷,![]() 與
與![]() 哪一個更適合作為日供應量
哪一個更適合作為日供應量![]() 與單價
與單價![]() 之間的回歸方程;(給出判斷即可,不必說明理由);
之間的回歸方程;(給出判斷即可,不必說明理由);
(2)根據(1)的判斷結果以及參考數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)該地區有![]() 個酒店,其中
個酒店,其中![]() 個酒店每日對蔬菜的需求量在
個酒店每日對蔬菜的需求量在![]() 以下,
以下,![]() 個酒店對蔬菜的需求量在
個酒店對蔬菜的需求量在![]() 以上,從這
以上,從這![]() 個酒店中任取
個酒店中任取![]() 個進行調查,求恰有
個進行調查,求恰有![]() 個酒店對蔬菜需求量在
個酒店對蔬菜需求量在![]() 以上的概率.
以上的概率.
參考公式及數據:
對于一組數據![]() ,
,![]() ...
...![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為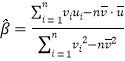 ,
,![]()

其中:![]() ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數
上是增函數![]() 若函數
若函數![]() ,利用上述性質,
,利用上述性質,
![]() Ⅰ
Ⅰ![]() 當
當![]() 時,求
時,求![]() 的單調遞增區間
的單調遞增區間![]() 只需判定單調區間,不需要證明
只需判定單調區間,不需要證明![]() ;
;
![]() Ⅱ
Ⅱ![]() 設
設![]() 在區間
在區間![]() 上最大值為
上最大值為![]() ,求
,求![]() 的解析式;
的解析式;
![]() Ⅲ
Ⅲ![]() 若方程
若方程![]() 恰有四解,求實數a的取值范圍.
恰有四解,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為加快新能源汽車產業發展,推進節能減排,國家對消費者購買新能源汽車給予補貼,其中對純電動乘用車補貼標準如下表:
新能源汽車補貼標準 | |||
車輛類型 | 續駛里程R(公里) | ||
80≤R<150 | 150≤R<250 | R≥250 | |
純電動乘用車 | 3.5萬元/輛 | 5萬元/輛 | 6萬元/輛 |
某校研究性學習小組,從汽車市場上隨機選取了M輛純電動乘用車,根據其續駛里程R(單次充電后能行駛的最大里程)作出了頻率與頻數的統計表:
分組 | 頻數 | 頻率 |
80≤R<150 | 2 | 0.2 |
150≤R<250 | 5 | x |
R≥250 | y | z |
合計 | M | 1 |
(Ⅰ)求x,y,z,M的值;
(Ⅱ)若從這M輛純電動乘用車中任選2輛,求選到的2輛車續駛里程都不低于150公里的概率;
(Ⅲ)若以頻率作為概率,設X為購買一輛純電動乘用車獲得的補貼,求X的分布列和數學期望EX.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)+1(A>0,ω>0,|φ|< ![]() ),圖象上有一個最低點是P(﹣
),圖象上有一個最低點是P(﹣ ![]() ,﹣1),對于f(x1)=1,f(x2)=3,|x1﹣x2|的最小值為
,﹣1),對于f(x1)=1,f(x2)=3,|x1﹣x2|的最小值為 ![]() . (Ⅰ)若f(α+
. (Ⅰ)若f(α+ ![]() )=
)= ![]() ,且α為第三象限的角,求sinα+cosα的值;
,且α為第三象限的角,求sinα+cosα的值;
(Ⅱ)討論y=f(x)+m在區間[0, ![]() ]上零點的情況.
]上零點的情況.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com