
第26屆世界大學生夏季運動會將于2011年8月12日至23日在深圳舉行,為了搞好接待工作,組委會在某學院招募了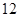 名男志愿者和
名男志愿者和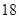 名女志愿者,調查發現,這
名女志愿者,調查發現,這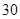 名志愿者的身高如下:(單位:cm )
名志愿者的身高如下:(單位:cm )

 男
女
男
女
 9 15 7 7 8 9
9
9 15 7 7 8 9
9
9 8 16 1 2 4 5 8 9
8 6 5 0 17 2 3 4 5 6
7 4 2 1 18 0 1
1 19
若身高在 cm以上(包括
cm以上(包括 cm)定義為“高個子”,身高在
cm)定義為“高個子”,身高在 cm以下定義為“非高個子”,且只有“女高個子”才能擔任“禮儀小姐”.
cm以下定義為“非高個子”,且只有“女高個子”才能擔任“禮儀小姐”.
(1)如果用分層抽樣的方法從“高個子”和“非高個子”中抽取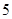 人,再從這
人,再從這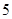 人中選
人中選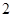 人,則至少有一人是“高個子”的概率是多少?
人,則至少有一人是“高個子”的概率是多少?
(2)若從所有“高個子”中選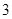 名志愿者,用
名志愿者,用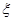 表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出
表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出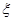 的分布列,并求
的分布列,并求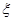 的數學期望.
的數學期望.
(1)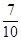 (2)數學期望:
(2)數學期望: ,分布列見解析
,分布列見解析
【解析】本題主要考查莖葉圖、分層抽樣、隨機事件的概率、對立事件的概率、隨機變量的分布列以及數學期望等基礎知識,考查運用概率統計知識解決簡單實際問題的數據處理能力和應用意識
(1)由題意及莖葉圖,有“高個子”12人,“非高個子”18人,利用用分層抽樣的方法,每個人被抽中的概率是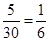 ,利用對立事件即可;
,利用對立事件即可;
(2)由于從所有“高個子”中選3名志愿者,用ξ表示所選志愿者中能擔任“禮儀小姐”的人數,利用離散型隨機變量的定義及題意可知ξ的取值為0,1,2,3在利用古典概型的概率公式求出每一個值對應事件的概率,有期望的公式求出即可.
解:(1)根據莖葉圖,有“高個子”12人,“非高個子”18人,
用分層抽樣的方法,每個人被抽中的概率是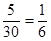 ,
,
所以選中的“高個子”有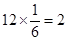 人,“非高個子”有
人,“非高個子”有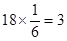 人.
人.
用事件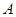 表示“至少有一名“高個子”被選中”,則它的對立事件
表示“至少有一名“高個子”被選中”,則它的對立事件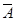 表示“沒有一名“高個子”被選中”,
表示“沒有一名“高個子”被選中”,
則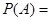
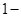
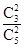
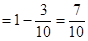 .因此,至少有一人是“高個子”的概率是
.因此,至少有一人是“高個子”的概率是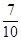 .
.
(2)依題意,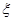 的取值為
的取值為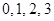 .
.
 ,
, 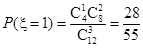 ,
,
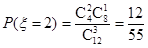 ,
, 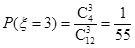 .
.
因此,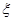 的分布列如下:
的分布列如下:
|
|
|
|
|
|
|
|
|
|
|
|
 .
.


科目:高中數學 來源: 題型:
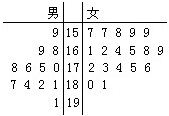 第26屆世界大學生夏季運動會將于2011年8月12日到23日在深圳舉行,為了搞好接待工作,組委會在某學院招募了12名男志愿者和18名女志愿者.將這30名志愿者的身高編成如右所示的莖葉圖(單位:cm):若身高在175cm以上(包括175cm)定義為“高個子”,身高在175cm以下(不包括175cm)定義為“非高個子”,且只有“女高個子”才擔任“禮儀小姐”.
第26屆世界大學生夏季運動會將于2011年8月12日到23日在深圳舉行,為了搞好接待工作,組委會在某學院招募了12名男志愿者和18名女志愿者.將這30名志愿者的身高編成如右所示的莖葉圖(單位:cm):若身高在175cm以上(包括175cm)定義為“高個子”,身高在175cm以下(不包括175cm)定義為“非高個子”,且只有“女高個子”才擔任“禮儀小姐”.查看答案和解析>>
科目:高中數學 來源: 題型:
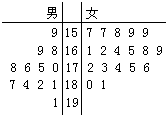 第26屆世界大學生夏季運動會將于2011年8月12日到23日在中國廣東舉行,為了搞好接待工作,組委會在某學院招募了12名男志愿者和18名女志愿者.將這30名志愿者的身高編成如右所示的莖葉圖(單位:cm):若身高在175cm以上(包括175cm)定義為“高個子”,身高在175cm以下(不包括175cm)定義為“非高個子”,且只有“女高個子”才擔任“禮儀小姐”.若從所有“高個子”
第26屆世界大學生夏季運動會將于2011年8月12日到23日在中國廣東舉行,為了搞好接待工作,組委會在某學院招募了12名男志愿者和18名女志愿者.將這30名志愿者的身高編成如右所示的莖葉圖(單位:cm):若身高在175cm以上(包括175cm)定義為“高個子”,身高在175cm以下(不包括175cm)定義為“非高個子”,且只有“女高個子”才擔任“禮儀小姐”.若從所有“高個子”查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源:2011屆廣東省高考猜押題卷文科數學(三)解析版 題型:解答題
(本小題滿分12分)
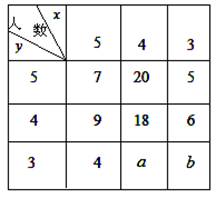
第26屆世界大學生夏季運動會將于2011年8月12日到23日在深圳舉行,為了搞好接待工作,組委會決定對禮儀小姐進行培訓.已知禮儀小姐培訓班的項目A與項目B成績抽樣統計表如下,抽出禮儀小姐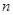 人,成績只有
人,成績只有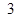 、
、 、
、 三種分值,設
三種分值,設 分別表示項目A與項目B成績.例如:表中項目A成績為
分別表示項目A與項目B成績.例如:表中項目A成績為 分的共7+9+4=20人.已知
分的共7+9+4=20人.已知 且
且 的概率是
的概率是 .
.
(I)求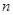 ;
;
(II)若在該樣本中,再按項目B的成績分層抽樣抽出 名禮儀小姐,則
名禮儀小姐,則 的禮儀小姐中應抽多少人?
的禮儀小姐中應抽多少人?
(Ⅲ)已知 ,
, ,項目B為3分的禮儀小姐中,求項目A得3分的人數比得4分人數多的概率.
,項目B為3分的禮儀小姐中,求項目A得3分的人數比得4分人數多的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com