
 ,OA⊥底面ABCD,OA=2,M為OA的中點(diǎn),N為BC的中點(diǎn).
,OA⊥底面ABCD,OA=2,M為OA的中點(diǎn),N為BC的中點(diǎn).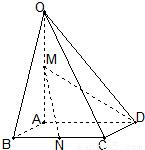
 ,
, ,而MD利用勾股定理求得等于
,而MD利用勾股定理求得等于 ,在直角三角形中,利用三角函數(shù)定義求出即可.
,在直角三角形中,利用三角函數(shù)定義求出即可.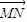 ,
,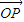 ,
,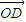 的坐標(biāo)表示.設(shè)平面OCD的法向量為
的坐標(biāo)表示.設(shè)平面OCD的法向量為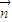 =(x,y,z),則
=(x,y,z),則 ,
,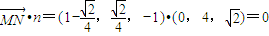 ,∴MN∥平面OCD
,∴MN∥平面OCD 和
和 ,利用a•b=|a||b|cosα求出叫即可.
,利用a•b=|a||b|cosα求出叫即可. 在向量
在向量 上的投影的絕對(duì)值,由
上的投影的絕對(duì)值,由 ,
, .所以點(diǎn)B到平面OCD的距離為
.所以點(diǎn)B到平面OCD的距離為 .
. 解:方法一(綜合法)
解:方法一(綜合法) ,∴
,∴ ,
, ,
,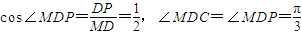
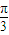 .
.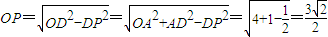 ,
,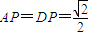 ,
, ,所以點(diǎn)B到平面OCD的距離為
,所以點(diǎn)B到平面OCD的距離為 .
. 方法二(向量法)
方法二(向量法) ,
, ,
,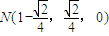
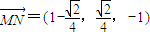 ,
, ,
,
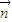 •
•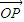 =0,
=0, •
•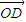 =0
=0
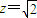 ,解得
,解得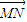 •
•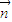 =(
=( ,
,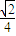 ,-1)•(0,4,
,-1)•(0,4, )=0,
)=0,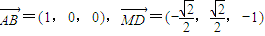
 ,
,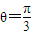 ,AB與MD所成角的大小為
,AB與MD所成角的大小為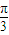 .
.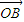 在向量
在向量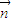 =(0,4,
=(0,4,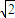 )上的投影的絕對(duì)值,
)上的投影的絕對(duì)值, ,得d=
,得d=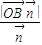 =
=
 .
.


| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
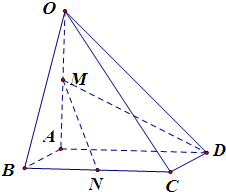 如圖,在四棱錐O-ABCD中,底面ABCD是邊長(zhǎng)為1的正方形,OA⊥底面ABCD,OA=2,M為OA的中點(diǎn),N為BC中點(diǎn),以A為原點(diǎn),建立適當(dāng)?shù)目臻g直角坐標(biāo)系,利用空間向量解答以下問題
如圖,在四棱錐O-ABCD中,底面ABCD是邊長(zhǎng)為1的正方形,OA⊥底面ABCD,OA=2,M為OA的中點(diǎn),N為BC中點(diǎn),以A為原點(diǎn),建立適當(dāng)?shù)目臻g直角坐標(biāo)系,利用空間向量解答以下問題查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
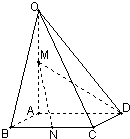 如圖,在四棱錐O-ABCD中,底面ABCD四邊長(zhǎng)為1的菱形,∠ABC=
如圖,在四棱錐O-ABCD中,底面ABCD四邊長(zhǎng)為1的菱形,∠ABC=| π | 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在四棱錐O-ABCD中,底面ABCD四邊長(zhǎng)為1的菱形,∠ABC=
如圖,在四棱錐O-ABCD中,底面ABCD四邊長(zhǎng)為1的菱形,∠ABC=| π | 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在四棱錐O-ABCD中,底面ABCD四邊長(zhǎng)為1的菱形,∠ABC=
如圖,在四棱錐O-ABCD中,底面ABCD四邊長(zhǎng)為1的菱形,∠ABC=| π | 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:江蘇同步題 題型:解答題
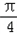 ,OA⊥底面ABCD,OA=2,M為OA的中點(diǎn),N為BC的中點(diǎn).
,OA⊥底面ABCD,OA=2,M為OA的中點(diǎn),N為BC的中點(diǎn).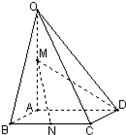
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com