【題目】設
為三次函數，且其圖象關于原點對稱，當
時，
的極小值為-1，則
（1）函數的解析式
__________；
（2）函數的單調遞增區間為___________。
【答案】（1）
（2）
和
【解析】
（1）先利用待定系數法設出f（x）的解析式，再根據奇偶性以及極值建立等式關系，求出參數即可；
（2）利用導數研究函數的單調性，求出函數
的單調遞增
（1）設f（x）=ax3+bx2+cx+d（a≠0）
∵其圖象關于原點對稱，即f（-x）=-f（x）
得-ax3+bx2-cx+d=-ax3-bx2-cx-d
∴b=d=0，
則有f（x）=ax3+cx
由f′（x）=3ax2+c，依題意得
∴
由①②得a=4，c=-3故所求的解析式為：f（x）=4x3-3x．
（2）由（1）可得f（x）=4x3-3x．則令f′（x）=12x2-3＞0
解得：
或
，即函數的單調遞增區間為和.
即答案為(1). (2). 和.
名師點撥卷系列答案科目：高中數學 來源： 題型：
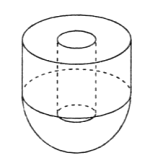
【題目】如圖所示，某幾何體由底面半徑和高均為5的圓柱與半徑為5的半球面對接而成，該封閉幾何體內部放入一個小圓柱體，且圓柱體的上下底面均與外層圓柱的底面平行，則小圓柱體積的最大值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高一舉行了一次數學競賽，為了了解本次競賽學生的成績情況，從中抽取了部分學生的分數（得分取正整數，滿分為
）作為樣本（樣本容量為
）進行統計，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分組作出頻率分布直方圖,已知得分在[50，60），[90，100]的頻數分別為8，2.
（1）求樣本容量
和頻率分布直方圖中的
的值；
（2）估計本次競賽學生成績的中位數；
（3）在選取的樣本中，從競賽成績在
分以上（含
分）的學生中隨機抽取
名學生，求所抽取的
名學生中至少有一人得分在
內的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
，
且
.
（1）若
為整數，且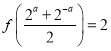
，試確定一個滿足條件的的值；
（2）設
的反函數為
，若
，試確定的取值范圍；
（3）若
，此時的反函數為，令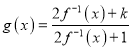
，若對一切實數
，
，
，不等式
恒成立，試確定實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】f（x）是定義在D上的函數，若對任何實數α∈（0，1）以及D中的任意兩數x1，x2，恒有f（αx1+（1﹣α）x2）≤αf（x1）+（1﹣α）f（x2），則稱f（x）為定義在D上的C函數.
（1）試判斷函數f1（x）＝x2，
中哪些是各自定義域上的C函數，并說明理由；
（2）若f（x）是定義域為
的函數且最小正周期為T，試證明f（x）不是R上的C函數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
（1）若對任意
，
且
，都有
，求實數
的取值范圍；
（2）在第（1）問求出的實數的范圍內，若存在一個與有關的負數
，使得對任意
時
恒成立，求的最小值及相應的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是某電商2019年12月1日至12月16日的日銷售量（單位：件）統計圖，銷量小于100稱為該商品滯銷，銷量大于200稱為該商品暢銷，則下列關于該商品在這16天的銷量的說法不正確的是( )
A.該商品出現過連續4天暢銷
B.該商品暢銷的頻率為0.5
C.相鄰兩天該商品銷量之差的最大值為195
D.該商品銷量的平均數小于200
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
