
設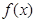 是定義在
是定義在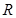 上以
上以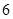 為周期的函數,
為周期的函數,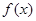 在
在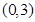 內單調遞減,且
內單調遞減,且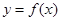 的圖象關于直線
的圖象關于直線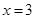 對稱,則下面正確的結論是( )
對稱,則下面正確的結論是( )
A.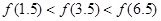 | B.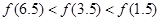 |
C.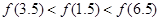 | D.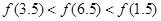 |
B
解析考點:奇偶函數圖象的對稱性;函數單調性的性質;函數的周期性.
專題:計算題.
分析:由函數f(x)的周期為6,從而有f(x+6)=f(x),所以有f(6.5)=f(0.5),f(3.5)=f(2.5),又因為0<0.5<1.5<2.5<3,且函數在(0,3)內單調遞減,從而判斷大小
解答:解:f(x)在R上以6為周期,對稱軸為x=3,且在(0,3)內單調遞減,f(3.5)=f(2.5),f(6.5)=f(0.5)
∵0.5<1.5<2.5
∴f(2.5)<f(1.5)<f(0.5)
即f(3.5)<f(1.5)<f(6.5)
故選 B
點評:本題主要考查了函數的周期性與單調性的綜合運用,利用周期性把所要比較的變量轉化到同一單調區間,利用函數的單調性比較函數值的大小,是解決此類問題的常用方法.


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:高中數學 來源:2010-2011學年重慶市七區高三第一次調研測試數學文卷 題型:選擇題
設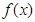 是定義在
是定義在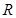 上以
上以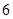 為周期的函數,
為周期的函數,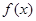 在
在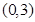 內單調遞減,且
內單調遞減,且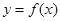 的圖象關于直線
的圖象關于直線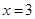 對稱,則下面正確的結論是(
)
對稱,則下面正確的結論是(
)
A.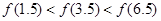 B.
B.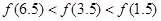
C.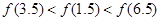 D.
D.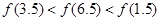
查看答案和解析>>
科目:高中數學 來源:2010-2011學年山東省高三第一次質量檢測理科數學卷 題型:選擇題
設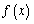 是定義在
是定義在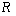 上以
上以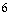 為周期的函數,函數
為周期的函數,函數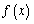 在
在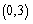 上單調遞減,且
上單調遞減,且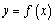 的圖像關于直線
的圖像關于直線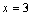 對稱,則下面結論中正確的是 (
)
對稱,則下面結論中正確的是 (
)
A. 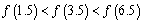 B.
B. 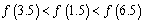
C.  D.
D. 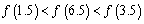
查看答案和解析>>
科目:高中數學 來源:2010-2011學年山東省高三第一次質量檢測理科數學卷 題型:選擇題
設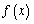 是定義在
是定義在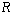 上以
上以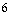 為周期的函數,函數
為周期的函數,函數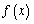 在
在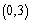 上單調遞減,且
上單調遞減,且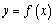 的圖像關于直線
的圖像關于直線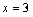 對稱,則下面結論中正確的是 (
)
對稱,則下面結論中正確的是 (
)
A. 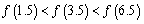 B.
B. 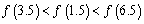
C. 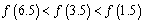 D.
D. 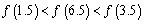
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com