設f(x)是定義在R上的函數,對任意x,y∈R有f(x+y)=f(x)+f(y)-1,當x>0時,f(x)>1,且f(3)=4;
(1)求f(1),f(4)的值;
(2)判斷并證明f(x)的單調性;
(3)若關于x的不等式f(|x|x+a2x+a)<f(f(4)•x)的解集中最大的整數為2,求實數a的取值范圍.
解:(1)由題意可得f(3)=f(2)+f(1)-1=4,f(2)=2f(1)-1
∴3f(1)-2=4,即f(1)=2,f(2)=3,f(3)=4,f(4)=2f(2)-1=5
(2)由(1)可得函數為單調遞增的函數
證明如下:設a>0,則x+a>x
∵由題意可得,當x>0時,f(x)>1
∴f(a)>1
由已知可得,f(x+a)-f(x)=f(x)+f(a)-f(x)-1=f(a)-1>0
∴f(x+a)>f(x)
由函數的單調性的定義可知函數單調遞增
(3)∵f(|x|x+a
2x+a)<f(f(4)•x)
由(2)中函數單調遞增且f(4)=5可得|x|x+a
2x+a<5x
當x>0可得,x
2+(a
2-5)x+a<0的解集中的最大整數為2
令g(x)=x
2+(a
2-5)x+a,則
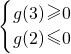
即
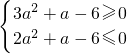
解可得

當x<0時,x
2+(5-a
2)x-a>0的解集中的最大整數為2,此時不符合題意
分析:(1)由題意可利用賦值求解f(1),f(4)
(2)利用函數單調性的定義:設a>0,則x+a>x,結合由已知可得,f(x+a)-f(x)=f(x)+f(a)-f(x)-1=f(a)-1>0從而可證
(3)結合(1)f(4)=5,及(2)中函數的單調性及f(|x|x+a
2x+a)<f(f(4)•x)可得
當x>0可得,x
2+(a
2-5)x+a<0的解集中的最大整數為2,令g(x)=x
2+(a
2-5)x+a,則
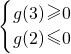
解不等式可求
當x<0時,此時不符合題意
點評:本題主要考查了抽象函數中利用賦值求解函數值及利用函數的單調性的定義判斷函數的單調性,解不等式,屬于函數知識的綜合應用.

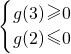
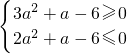 解可得
解可得
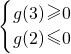 解不等式可求
解不等式可求

 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案