
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的極小值;
的極小值;
(Ⅱ)當![]() 時,過坐標原點
時,過坐標原點![]() 作曲線
作曲線![]() 的切線,設切點為
的切線,設切點為![]() ,求實數
,求實數![]() 的值;
的值;
(Ⅲ)設定義在![]() 上的函數
上的函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() :
: ![]() ,當
,當![]() 時,若
時,若![]() 在
在![]() 內恒成立,則稱
內恒成立,則稱![]() 為函數
為函數![]() 的“轉點”.當
的“轉點”.當![]() 時,試問函數
時,試問函數![]() 是否存在“轉點”.若存在,請求出“轉點”的橫坐標,若不存在,請說明理由.
是否存在“轉點”.若存在,請求出“轉點”的橫坐標,若不存在,請說明理由.
【答案】(Ⅰ)-2;(Ⅱ) ![]() ;(Ⅲ)參考解析
;(Ⅲ)參考解析
【解析】試題分析:(Ⅰ)先求導數,再求導數零點,最后根據導數符號變化規律,確定極小值,(Ⅱ)根據導數幾何意義得切線的斜率等于切點處導數值,可得關于![]() 的方程,再利用導數研究單調性確定方程解的個數,最后根據估值得方程的解,(Ⅲ)先求切線方程得
的方程,再利用導數研究單調性確定方程解的個數,最后根據估值得方程的解,(Ⅲ)先求切線方程得![]() ,再求函數
,再求函數![]() 導數,最后根據導函數的兩個零點必須相同得“轉點”.
導數,最后根據導函數的兩個零點必須相同得“轉點”.
試題解析:(Ⅰ)當![]() 時,
時, ![]() ,
,
當![]() 時
時![]() ;當
;當![]() 時
時![]() ;當
;當![]() 時
時![]() .
.
所以當![]() 時,
時, ![]() 取到極小值-2.
取到極小值-2.
(Ⅱ)![]() ,所以切線的斜率
,所以切線的斜率![]() ,
,
整理得![]() ,顯然
,顯然![]() 是這個方程的解,
是這個方程的解,
又因為![]() 在
在![]() 上是增函數,
上是增函數,
所以方程![]() 有唯一實數解,故
有唯一實數解,故![]() .
.
(Ⅲ)當![]() 時,函數
時,函數![]() 在其圖象上一點
在其圖象上一點![]() 處的切線方程為
處的切線方程為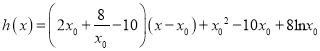 ,
,
設![]() ,則
,則![]() ,
, 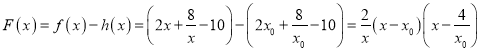 ,
,
若![]() ,
, ![]() 在
在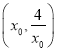 上單調遞減,所以當
上單調遞減,所以當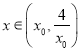 時
時![]() ,此時
,此時![]() ;
;
所以![]() 在
在![]() 上不存在“轉點”.
上不存在“轉點”.
若![]() 時,
時, ![]() 在
在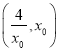 上單調遞減,所以當
上單調遞減,所以當 時
時![]() ,此時
,此時![]() ,所以
,所以![]() 在
在![]() 上不存在“轉點”.
上不存在“轉點”.
若![]() 時
時![]() ,即
,即![]() 在
在![]() 上是增函數,
上是增函數,
當![]() 時,
時, ![]() ,
,
當![]() 時,
時, ![]() ,即點
,即點![]() 為“轉點”,
為“轉點”,
故函數![]() 存在“轉點”,且2是“轉點”的橫坐標.
存在“轉點”,且2是“轉點”的橫坐標.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】某校對高一年級學生寒假參加社區服務的次數進行了統計,隨機抽取了![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數,根據此數據作出了頻率分布統計表和頻率分布直方圖如下:
名學生參加社區服務的次數,根據此數據作出了頻率分布統計表和頻率分布直方圖如下:

(1)求表中![]() 的值和頻率分布直方圖中
的值和頻率分布直方圖中![]() 的值,并根據頻率分布直方圖估計該校高一學生寒假參加社區服務次數的中位數;
的值,并根據頻率分布直方圖估計該校高一學生寒假參加社區服務次數的中位數;
(2)如果用分層抽樣的方法從樣本服務次數在![]() 和
和![]() 的人中共抽取6人,再從這6人中選2人,求2人服務次數都在
的人中共抽取6人,再從這6人中選2人,求2人服務次數都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]()
(1)求函數![]() 的單調遞減區間;
的單調遞減區間;
(2)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有兩個不等的根,求實數
上有兩個不等的根,求實數![]() 的取值范圍;
的取值范圍;
(3)若存在![]() ,當
,當![]() 時,恒有
時,恒有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數,
為常數, ![]() 是自然對數的底數),曲線
是自然對數的底數),曲線![]() 在點
在點![]() 處的切線方程是
處的切線方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的單調區間;
的單調區間;
(3)設![]() (其中
(其中![]() 為
為![]() 的導函數)。證明:對任意
的導函數)。證明:對任意![]() ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在遂寧市中央商務區的街道,有一中年人吆喝“送錢”,只見他手拿一黑色小布袋,袋中有3只黃色、2只白色的乒乓球(其體積,質地完全相同),旁邊立著一塊小黑板寫道:
摸球方法:從袋中隨機摸出3個球,若摸得統一顏色的3個球,攤主送個摸球者10元錢;若摸得非同一顏色的3個球。摸球者付給攤主2元錢。
(1)摸出的3個球中至少有1個白球的概率是多少?
(2)假定一天中有100人次摸獎,試從概率的角度估算一下這個攤主一個月(按30天計)能賺多少錢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com