
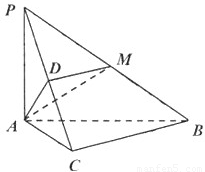
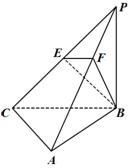
如圖,三棱錐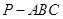 中,
中,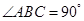 ,
,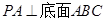
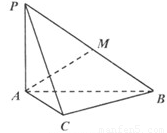
(Ⅰ)求證: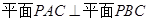 ;
;
(Ⅱ)若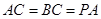 ,
,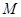 是
是 的中點(diǎn),求
的中點(diǎn),求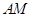 與平面
與平面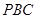 所成角的正切值
所成角的正切值
(Ⅰ)證明略;(Ⅱ)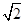
【解析】
試題分析:(Ⅰ)根據(jù)直線與平面垂直的判定定理,只要找到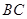 和平面
和平面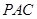 中兩條相交直線垂直就可以證明直線和平面垂直,那么再由平面和平面垂直的判定定理可知
中兩條相交直線垂直就可以證明直線和平面垂直,那么再由平面和平面垂直的判定定理可知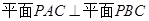 ,證明中要把條件到結(jié)論敘述清楚;(Ⅱ)先根據(jù)
,證明中要把條件到結(jié)論敘述清楚;(Ⅱ)先根據(jù)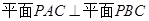 這個(gè)條件做輔助線構(gòu)造出所求的線面角,再在三角形中根據(jù)解三角形的方法求得線面角的正切值,一定要注意線面角要找準(zhǔn),不能亂構(gòu)造
這個(gè)條件做輔助線構(gòu)造出所求的線面角,再在三角形中根據(jù)解三角形的方法求得線面角的正切值,一定要注意線面角要找準(zhǔn),不能亂構(gòu)造
試題解析:解:(Ⅰ)因?yàn)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2013122609205845319205/SYS201312260921484030661186_DA.files/image005.png">,所以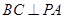 2分
2分
又因?yàn)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2013122609205845319205/SYS201312260921484030661186_DA.files/image007.png">,即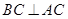
所以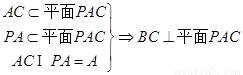 4分
4分
又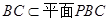 ,所以
,所以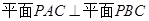 6分
6分
(Ⅱ)取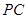 中點(diǎn)
中點(diǎn)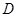 ,連
,連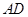 ,則
,則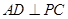
又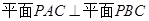 ,所以
,所以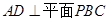 ,連結(jié)
,連結(jié)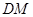 ,
,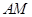 ,
,
則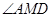 就是
就是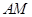 與平面
與平面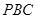 所成的角 10分
所成的角 10分
設(shè)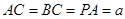 ,則
,則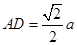 ,
,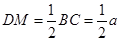 ,
,
所以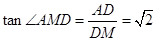 15分
15分
考點(diǎn):1、直線與平面垂直的判定;2、平面與平面垂直的判定;3、直線與平面所成的角


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2012-2013學(xué)年河南鄭州盛同學(xué)校高三4月模擬考試文科數(shù)學(xué)試卷(解析版) 題型:解答題
如圖,三棱錐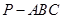 中,
中,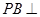 底面ABC于B,
底面ABC于B,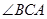 =900,
=900,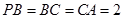 ,點(diǎn)E、F分別是PC、AP的中點(diǎn)。
,點(diǎn)E、F分別是PC、AP的中點(diǎn)。

(1)求證:側(cè)面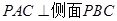 ;
;
(2)求異面直線AE與BF所成的角;
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2012-2013學(xué)年遼寧省沈陽(yáng)市高三高考領(lǐng)航考試(一)理科數(shù)學(xué)試卷(解析版) 題型:填空題
如圖,在三棱錐 中,
中,  、
、 、
、 兩兩垂直, 且
兩兩垂直, 且 .設(shè)
.設(shè) 是底面
是底面 內(nèi)一點(diǎn),定義
內(nèi)一點(diǎn),定義 ,其中
,其中 、
、 、
、 分別是三棱錐M-PAB、
三棱錐M-PBC、三棱錐M-PCA的體積.若
分別是三棱錐M-PAB、
三棱錐M-PBC、三棱錐M-PCA的體積.若 ,且
,且 恒成立,則正實(shí)數(shù)
恒成立,則正實(shí)數(shù) 的最小值為___ ___.
的最小值為___ ___.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年廣東省佛山市高三教學(xué)質(zhì)量檢測(cè)(一)理科數(shù)學(xué) 題型:解答題
如圖,三棱錐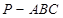 中,
中,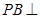 底面
底面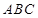 ,
,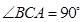 ,
,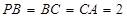 ,
,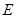 為
為 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)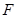 在
在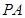 上,且
上,且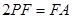 .
.
(1)求證:平面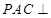 平面
平面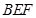 ;
;
(2)求平面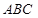 與平面
與平面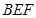 所成的二面角的平面角(銳角)的余弦值.
所成的二面角的平面角(銳角)的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年廣東省佛山市高三教學(xué)質(zhì)量檢測(cè)(一)文科數(shù)學(xué) 題型:解答題
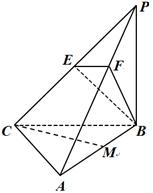
如圖,三棱錐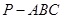 中,
中,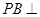 底面
底面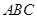 ,
,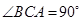 ,
, 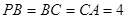 ,
,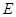 為
為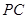 的中點(diǎn),
的中點(diǎn),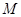 為
為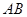 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)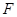 在
在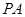 上,且
上,且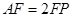 .
.
(1)求證: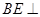 平面
平面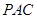 ;
;
(2)求證: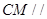 平面
平面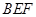 ;
;
(3)求三棱錐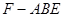 的體積.
的體積.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com