【題目】已知函
，其中
.
（Ⅰ）若
，求曲線
在點（2，f（2））處的切線方程；
（Ⅱ）若在區間
上，f（x）>0恒成立，求a的取值范圍.
【答案】(1) y=6x-9 ;(2) 0<a<5.
【解析】
（Ⅰ）當
時，代入函數的解析式求得
和
，進而求得
，即切線的斜率為
，再利用直線的點斜式方程，即可求解；
（Ⅱ）求出
時
的值，分
和
兩種情況討論函數的增減性分別取得
和
，及和
都大于
，聯立分別求解
的解集，取并集，即可得到的取值范圍.
（Ⅰ）解：當a=1時，f（x）=
，f（2）=3；
, 
.
所以曲線y=f（x）在點（2，f（2））處的切線方程為y-3=6（x-2），即y=6x-9
（Ⅱ）解：
.令
，解得x=0或x=
以下分兩種情況討論：
若
，當x變化時，
，
的變化情況如下表：
X |
| 0 |
|
f’(x) | + | 0 | - |
f(x) |
| 極大值 |
|
當
等價于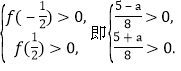
解不等式組得-5<a<5.因此
.
(2)若a>2，則
.當x變化時，，的變化情況如下表：
X |
| 0 |
|
|
|
f’(x) | + | 0 | - | 0 | + |
f(x) |
| 極大值 |
| 極小值 |
|
當
時，f（x）>0等價于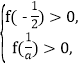
即
解不等式組得
或
.因此2<a<5
綜合（1）和（2），可知a的取值范圍為0<a<5.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】（本小題共l2分）
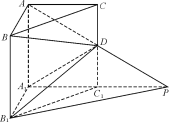
如圖，在直三棱柱ABC－A1B1C1中，∠BAC=90°，AB=AC=AA1=1，延長A1C1至點P，使C1P＝A1C1，連接AP交棱CC1于D．
（Ⅰ）求證：PB1∥平面BDA1；
（Ⅱ）求二面角A－A1D－B的平面角的余弦值；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】高考復習經過二輪“見多識廣”之后，為了研究考前“限時搶分”強化訓練次數
與答題正確率
﹪的關系，對某校高三某班學生進行了關注統計，得到如下數據：
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
（1）求關于的線性回歸方程，并預測答題正確率是100﹪的強化訓練次數；
（2）若用
表示統計數據的“強化均值”（精確到整數），若“強化均值”的標準差在區間
內，則強化訓練有效，請問這個班的強化訓練是否有效？
附：回歸直線的斜率和截距的最小二乘法估計公式分別為：
，
＝
－
，
樣本數據
的標準差為：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某大學準備在開學時舉行一次大學一年級學生座談會，擬邀請20名來自本校機械工程學院、海洋學院、醫學院、經濟學院的學生參加，各學院邀請的學生數如下表所示：
學院 | 機械工程學院 | 海洋學院 | 醫學院 | 經濟學院 |
人數 | 4 | 6 | 4 | 6 |
（Ⅰ）從這20名學生中隨機選出3名學生發言，求這3名學生中任意兩個均不屬于同一學院的概率；
（Ⅱ）從這20名學生中隨機選出3名學生發言，設來自醫學院的學生數為ξ，求隨機變量ξ的概率分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
=1（a＞b＞0）的短軸長為2，離心率e= 
．
（Ⅰ）求橢圓C的方程；
（Ⅱ）若直線l：y=kx+m與橢圓交于不同的兩點A，B，與圓x2+y2= 
相切于點M．
（i）證明：OA⊥OB（O為坐標原點）；
（ii）設λ= 
，求實數λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）在R上存在導數f′（x），對任意的x∈R，有f（﹣x）+f（x）=x2 ， 且x∈（0，+∞）時，f′（x）＞x．若f（2﹣a）﹣f（a）≥2﹣2a，則實數a的取值范圍為（ ）
A.[1，+∞）
B.（﹣∞，1]
C.（﹣∞，2]
D.[2，+∞）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
