Question

如圖所示，在排成4×4方陣的16個點中，中心位置4個點在某圓內，其余12個點在圓外.從16個點中任選3點，作為三角形的頂點，其中至少有一個頂點在圓內的三角形共有多少個？

Answer 1

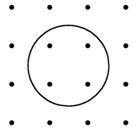
錯解1：16個點中任取3個有種方法，其中三個點都不在圓內的有種，故滿足題設條件的三角形有-=340個.

錯解2：要作出符合題意的三角形，從圓內四點中：

①任取3點，有種；

②任取2點，圓外取1點，有種；

③任取1點，圓外取2點，有種.

綜上可知，至少有一個頂點在圓內的三角形共有++=340個.

剖析：錯解1中不符合題意的還有兩種情形：一是4點共線，但其中任意3點至少有1點在圓內，這樣的4點有6種；還有就是只有3點共線，但其中恰有1點在圓內，這樣的3點有4種.因此，正確解法是：--6-4=312種.

錯解2錯在②③兩種情形，其中所取的3點可能是共線的.因此，要兼顧題中的兩個約束條件：所取三點可作成三角形；至少有一個點在圓內.因此正確解法是：從圓內四點中任取.

①3點，有種；

②2點，圓外12點中取1點，有種；

③1點，圓外12點中取2點，有（-4）種.

綜上可知，所求的三角形共有++（-4）=312個.