Question

13．若關于x的不等式4^x-log_ax＜0在區間（0，$\frac{1}{2}$]上恒成立，則實數a的取值范圍是（$\frac{\sqrt{2}}{2}$，1）．

Answer 1

分析 若關于x的不等式4^x-log_ax＜0在區間（0，$\frac{1}{2}$]上恒成立，則y=log_ax的圖象恒在y=4^x的圖象的上方，在同一坐標系中，分析畫出指數和對數函數的圖象，分析可得答案．

解答 解：當0＜x≤$\frac{1}{2}$時，函數y=4^x的圖象如下圖所示：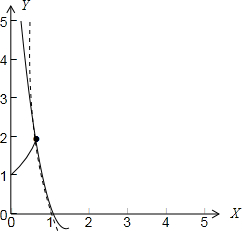

若不等式4^x-log_ax＜0在區間（0，$\frac{1}{2}$]上恒成立，即不等式4^x＜log_ax恒成立，
則y=log_ax的圖象恒在y=4^x的圖象的上方（如圖中虛線所示）
∵y=log_ax的圖象與y=4^x的圖象交于（$\frac{1}{2}$，2）點時，a=$\frac{\sqrt{2}}{2}$
故虛線所示的y=log_ax的圖象對應的底數a應滿足$\frac{\sqrt{2}}{2}$＜a＜1
故答案為：（$\frac{\sqrt{2}}{2}$，1）

點評 本題以指數函數與對數函數圖象與性質為載體考查了函數恒成立問題，其中熟練掌握指數函數和對數函數的圖象與性質是解答本題的關鍵．