
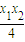 代入兩直線的斜率的乘積中求得結果為-1進而可推斷出PA⊥PB;判斷出條件的充分性;同時根據PA⊥PB推斷出
代入兩直線的斜率的乘積中求得結果為-1進而可推斷出PA⊥PB;判斷出條件的充分性;同時根據PA⊥PB推斷出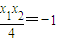 ,進而p在l上,判斷出條件的必要性,最后綜合可得答案.
,進而p在l上,判斷出條件的必要性,最后綜合可得答案.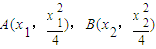 ,由導數不難知道直線PA,PB的斜率分別為
,由導數不難知道直線PA,PB的斜率分別為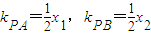 .進一步得PA:
.進一步得PA: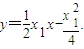 ①
①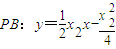 .②,由聯立①②可得點
.②,由聯立①②可得點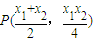 ,
,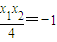 ,所以
,所以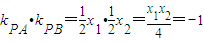 ,所以PA⊥PB;∴甲是乙的充分條件
,所以PA⊥PB;∴甲是乙的充分條件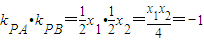 ,即yp=-1,從而點P在l上.∴甲是乙的必要條件,
,即yp=-1,從而點P在l上.∴甲是乙的必要條件,

 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| AF |
| FB |
| AB |
| FQ |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
|
|
|
| ||
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com