已知函數f(x)=x2-ax+b
(Ⅰ)【理科】若b=4時,f(x)≥0對x∈(0,4)恒成立,求a的范圍;
【文科】若b=4時,f(x)≥0對x∈R恒成立,求a的范圍;
(Ⅱ)若f(-1)≥0,f(0)≤0,f(2)≥0,求f(3)的范圍.
解:(Ⅰ)理科:∵若b=4時,f(x)≥0對x∈(0,4)恒成立,
∴f(x)=x
2-ax+4≥0,∴a≤
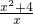
=x+

,求出x+

的最小值即可,
∵x+

≥2

=4(當x=2時等號成立);
∴a≤4;
文科:∵若b=4時,f(x)≥0對x∈R恒成立,也即x
2-ax+4≥0對x∈R恒成立,
∴△≤0即可,也即a
2-4×4≤0,∴-4≤a≤4;
(Ⅱ)∵f(x)=x
2-ax+b,f(-1)≥0,f(0)≤0,f(2)≥0,
可得
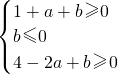
,目標函數z=f(3)=9-3a+b,
畫出可行域:可以令a=x,b=y,如下圖
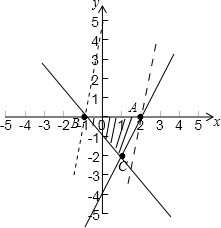
如圖在點A(2,0)處z取得最小值,在點B(-1,0)處取最大值,
∴z
min=9-6=3,z
max=9+3=12,
∴3≤f(3)≤12;
分析:(Ⅰ)理科:把b=4代入f(x),由題意,f(x)≥0對x∈(0,4)恒成立,可以利用分離常數法進行求解;
文科:文科f(x)≥0對x∈R恒成立,函數開口向上,要是函數f(x)恒大于0,只要△≤0即可;
(Ⅱ)第二問就是一個線性規劃問題,找出可行域和目標函數,畫出草圖即可求解;
點評:第一問比較簡單,用到了常數分離法,使問題簡單化,第二問要看出來這是一個線性規劃問題,就比較容易求解了;

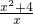 =x+
=x+ ,求出x+
,求出x+ 的最小值即可,
的最小值即可, ≥2
≥2 =4(當x=2時等號成立);
=4(當x=2時等號成立);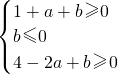 ,目標函數z=f(3)=9-3a+b,
,目標函數z=f(3)=9-3a+b,


 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<