
已知三條直線l1:2x-y+a=0(a>0),直線l2:4x-2y-1=0和直線l3:x+y-1=0,且l1與l2的距離是![]() .
.
(1)求a的值;
(2)能否找到一點P,使得P點同時滿足下列三個條件:
①P是第一象限的點;②P點到l1的距離是P點到l2的距離的![]() ;③P點到l1的距離與P點到l3的距離之比是
;③P點到l1的距離與P點到l3的距離之比是![]() ∶
∶![]() .若能,求P點坐標;若不能,說明理由.
.若能,求P點坐標;若不能,說明理由.
(1)a=3(2)點P![]() 即為同時滿足三個條件的點
即為同時滿足三個條件的點
(1)l2即為2x-y-![]() =0,
=0,
∴l1與l2的距離d=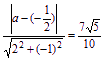 ,
,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
∵a>0,∴a=3.
(2)假設存在這樣的P點.
設點P(x0,y0),若P點滿足條件②,則P點在與l1、l2平行的直線l′:2x-y+C=0上,
且![]() =
=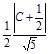 ,即C=
,即C=![]() 或C=
或C=![]() ,
,
∴2x0-y0+![]() =0或2x0-y0+
=0或2x0-y0+![]() =0;
=0;
若P點滿足條件③,由點到直線的距離公式![]() =
=![]() ×
×![]() ,
,
即|2x0-y0+3|=|x0+y0-1|,
∴x0-2y0+4=0或3x0+2=0;
由于P點在第一象限,∴3x0+2=0不滿足題意.
聯立方程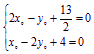 ,
,
解得![]() (舍去).
(舍去).
由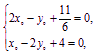 解得
解得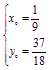
∴假設成立,點P![]() 即為同時滿足三個條件的點.
即為同時滿足三個條件的點.


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:
| 7 |
| 10 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
7
| ||
| 10 |
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
已知三條直線l1:2x-y+a=0(a>0),直線l2:-4x+2y+1=0和直線l3:x+y-1=0,且l1與l2的距離是![]()
![]() .
.
(1)求a的值;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)求l3到l1的角θ;
(3)能否找到一點P,使得P點同時滿足下列三個條件:①P是第一象限的點;②P點到l1的距離是P點到l2的距離的![]() ;③P點到l1的距離與P點到l3的距離之比是
;③P點到l1的距離與P點到l3的距離之比是![]() ∶
∶![]() ?若能,求P點坐標;若不能,請說明理由.
?若能,求P點坐標;若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)求實數a的值;
(2)能否找到一點P,使得P點同時滿足下列三個條件:①P是第一象限的點;②P點到直線l1的距離是P點到直線l2的距離的![]() ;③P點到直線l1的距離與P點到直線l3的距離之比為
;③P點到直線l1的距離與P點到直線l3的距離之比為![]() ∶
∶![]() .若能,求出點P的坐標;若不能,請說明理由.
.若能,求出點P的坐標;若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知三條直線l1:2x-y+3=0,直線l2:-4x+2y+1=0和直線l3:x+y-1=0.能否找到一點P,使得P點同時滿足下列三個條件:(1)P是第一象限的點;(2)P點到l1的距離是P點到l2的距離的![]() ;(3)P點到l1的距離與P點到l3的距離之比是
;(3)P點到l1的距離與P點到l3的距離之比是![]() .若能,求P點坐標;若不能,請說明理由.
.若能,求P點坐標;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com