解:(1)因為f(x)=

x
3+

ax
2+x+b(a≥0),
所以f′(x)=x
2+ax+1.
因為f(x)在x=-3處取到極大值-2,
所以
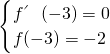
,即
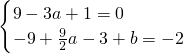
,
解得a=

,b=-5.
(2)由(1)可得:f′(x)=x
2+ax+1,
所以g(x)=e
-ax•f′(x)=
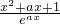
(x∈R),
所以g′(x)=-x[ax+(a
2-2)]e
-ax=-ax[x-(
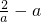
)]e
-ax.
①當a=0時,g′(x)=2x,
所以g(x)的單調(diào)遞增區(qū)間為(0,+∞),單調(diào)遞減區(qū)間為(-∞,0).
②當a>0時,令g′(x)=0解得x=0或x=
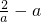
.
(i)當
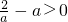
時,即
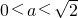
時,
則g′(x)>0的解集為
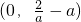
,g′(x)<0的解集為(-∞,0),(
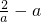
,+∞),
所以g(x)的單調(diào)遞增區(qū)間為
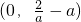
,單調(diào)遞減區(qū)間為(-∞,0),(
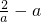
,+∞).
(ii)當

,即a=

時,則g′(x)=
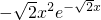
≤0,
所以g(x)在(-∞,+∞)上單調(diào)遞減.
(iii)當

,即a>

時,
則g′(x)>0的解集為
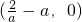
,g′(x)<0的解集為(-∞,
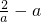
),(0,+∞).
所以g(x)的單調(diào)遞增區(qū)間為
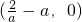
,單調(diào)遞減區(qū)間為(-∞,
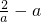
),(0,+∞).
總上所述:
當a=0時,g(x)的單調(diào)遞增區(qū)間為(0,+∞),單調(diào)遞減區(qū)間為(-∞,0).
當
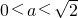
時,g(x)的單調(diào)遞增區(qū)間為
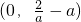
,單調(diào)遞減區(qū)間為(-∞,0),(
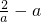
,+∞).
當a=

時,g(x)在(-∞,+∞)上單調(diào)遞減.
當a>

時,g(x)的單調(diào)遞增區(qū)間為
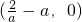
,單調(diào)遞減區(qū)間為(-∞,
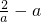
),(0,+∞).
分析:(1)根據(jù)題意得到:f′(x)=x
2+ax+1,結(jié)合f(x)在x=-3處取到極大值-2可得關(guān)于a與b的方程組,進而求出a與b的數(shù)值.
(2)由(1)可得:g′(x)=-x[ax+(a
2-2)]e
-ax=-ax[x-(
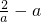
)]e
-ax,結(jié)合解一元二次不等式的知識對a進行分類討論,進而求出函數(shù)的得到區(qū)間.
點評:本題主要考查函數(shù)的單調(diào)性與其導(dǎo)函數(shù)的正負之間的關(guān)系,即當導(dǎo)函數(shù)大于0時原函數(shù)單調(diào)遞增,當導(dǎo)函數(shù)小于0時原函數(shù)單調(diào)遞減,以及考查含參數(shù)的一元二次不等式問題.

 x3+
x3+ ax2+x+b(a≥0)為函數(shù)f(x)的導(dǎo)函數(shù).
ax2+x+b(a≥0)為函數(shù)f(x)的導(dǎo)函數(shù). x3+
x3+ ax2+x+b(a≥0),
ax2+x+b(a≥0),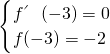 ,即
,即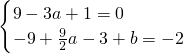 ,
, ,b=-5.
,b=-5.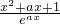 (x∈R),
(x∈R),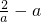 )]e-ax.
)]e-ax.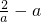 .
.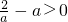 時,即
時,即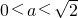 時,
時,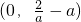 ,g′(x)<0的解集為(-∞,0),(
,g′(x)<0的解集為(-∞,0),(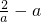 ,+∞),
,+∞),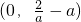 ,單調(diào)遞減區(qū)間為(-∞,0),(
,單調(diào)遞減區(qū)間為(-∞,0),(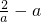 ,+∞).
,+∞). ,即a=
,即a= 時,則g′(x)=
時,則g′(x)=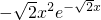 ≤0,
≤0, ,即a>
,即a> 時,
時,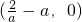 ,g′(x)<0的解集為(-∞,
,g′(x)<0的解集為(-∞,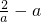 ),(0,+∞).
),(0,+∞).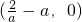 ,單調(diào)遞減區(qū)間為(-∞,
,單調(diào)遞減區(qū)間為(-∞,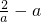 ),(0,+∞).
),(0,+∞).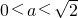 時,g(x)的單調(diào)遞增區(qū)間為
時,g(x)的單調(diào)遞增區(qū)間為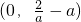 ,單調(diào)遞減區(qū)間為(-∞,0),(
,單調(diào)遞減區(qū)間為(-∞,0),(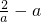 ,+∞).
,+∞). 時,g(x)在(-∞,+∞)上單調(diào)遞減.
時,g(x)在(-∞,+∞)上單調(diào)遞減. 時,g(x)的單調(diào)遞增區(qū)間為
時,g(x)的單調(diào)遞增區(qū)間為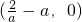 ,單調(diào)遞減區(qū)間為(-∞,
,單調(diào)遞減區(qū)間為(-∞,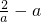 ),(0,+∞).
),(0,+∞).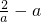 )]e-ax,結(jié)合解一元二次不等式的知識對a進行分類討論,進而求出函數(shù)的得到區(qū)間.
)]e-ax,結(jié)合解一元二次不等式的知識對a進行分類討論,進而求出函數(shù)的得到區(qū)間.

 百分學生作業(yè)本題練王系列答案
百分學生作業(yè)本題練王系列答案 互動課堂系列答案
互動課堂系列答案 已知函數(shù)f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數(shù)f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<