
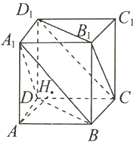
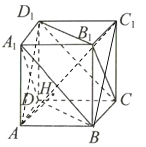
【題目】如圖,正方體![]() 的棱長為1,過
的棱長為1,過![]() 點作平面
點作平面![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,有下面三個結論:①點
,有下面三個結論:①點![]() 是
是![]() 的中心;②
的中心;②![]() 垂直于平面
垂直于平面![]() ;③直線
;③直線![]() 與直線
與直線![]() 所成的角是90°.其中正確結論的序號是_______.
所成的角是90°.其中正確結論的序號是_______.
【答案】①②③
【解析】
對于①,先利用線面垂直的性質,結合已知條件,得到![]() ,進而可判斷①;
,進而可判斷①;
對于②,由已知條件,根據面面平行的判定定理,得到平面![]() 平面
平面![]() ,再由
,再由![]() 垂直于平面
垂直于平面![]() ,即可判斷②;
,即可判斷②;
對于③,連接![]() ,根據線面垂直的判定定理,得到
,根據線面垂直的判定定理,得到![]() 平面
平面![]() ,即可得出
,即可得出![]() ,從而可判斷③
,從而可判斷③
對于①,因為![]() 平面
平面![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() 是
是![]() 的外心;
的外心;
又因為![]() 是等邊三角形,所以點
是等邊三角形,所以點![]() 是△
是△![]() 的中心.故①正確;
的中心.故①正確;
對于②,因為![]() ,
,![]() ,
,
所以![]() ,且
,且![]() ,所以四邊形
,所以四邊形![]() 是平行四邊形,所以
是平行四邊形,所以![]() .
.
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
同理可證![]() 平面
平面![]() .
.
又因為![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
又因為![]() 垂直于平面
垂直于平面![]() ,所以
,所以![]() 垂直于平面
垂直于平面![]() .故②正確;
.故②正確;
對于③,連接![]() .
.
因為四邊形![]() 是正方形,所以
是正方形,所以![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
又因為![]() ,所以
,所以![]() 平面
平面![]() .
.
又因為![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以直線![]() 與
與![]() 所成的角是90°.
所成的角是90°.
故答案為①②③


科目:高中數學 來源: 題型:
【題目】已知圓心在直線![]() 上的圓C經過
上的圓C經過![]() 點,且與直線
點,且與直線![]() 相切.
相切.
(1)求過點P且被圓C截得的弦長等于4的直線方程;
(2)過點P作兩條相異的直線分別與圓C交于A,B,若直線PA,PB的傾斜角互補,試判斷直線AB與OP的位置關系(O為坐標原點),并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,三國時代數學家趙爽在《周髀算經》中利用弦圖,給出了勾股定理的絕妙證明.圖中包含四個全等的直角三角形及一個小正方形(陰影),設直角三角形有一內角為![]() ,若向弦圖內隨機拋擲500顆米粒(大小忽略不計,取
,若向弦圖內隨機拋擲500顆米粒(大小忽略不計,取![]() ),則落在小正方形(陰影)內的米粒數大約為( )
),則落在小正方形(陰影)內的米粒數大約為( )
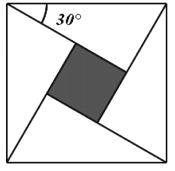
A. 134 B. 67 C. 200 D. 250
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了對某課題進行研究,分別從A,B,C三所高校中用分層隨機抽樣法抽取若干名教授組成研究小組,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中![]() )
)
(1)若A,B兩所高校中共抽取3名教授,B,C兩所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授數是高校A和C中抽取的教授總數的![]() ,求三所高校的教授的總人數.
,求三所高校的教授的總人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=8,BC=4,E為DC邊的中點,沿AE將△ADE折起,在折起過程中,有幾個正確( )

①ED⊥平面ACD ②CD⊥平面BED
③BD⊥平面ACD ④AD⊥平面BED
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年8月教育部、國家衛生健康委員會等八個部門聯合印發《綜合防控兒童青少年近視實話方案》中明確要求,為切實加強新時代兒童青少年近視防控工作,學校應嚴格組織全體學生每天上、下午各大做1次眼保健操.為了了解學校推廣眼保健操是否能有效預防近視,隨機從甲學校抽取了50名學生,再從乙學校選出與甲學校被抽取的50名學生視力情況一樣的50學生(期中甲學校每天安排學生做眼保健操,乙學校不安排做跟保健操),一段時間后檢測他們的視力情況并統計,若視力情況為1.0及以上,則認為該學生視力良好,否則認為該學生的視力一般,表1為甲學校視力情況的頻率分布表,表2為乙學校學生視力情況的頻率分布表,根據表格回答下列問題:
表1 甲學校學生視力情況的頻率分布表
視力情況 | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 |
頻 數 | 1 | 1 | 15 | 15 | 18 |
表2 乙學校學生視力情況的頻率分布表
視力情況 | 0.5 | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 |
頻 數 | 2 | 2 | 4 | 19 | 13 | 10 |
(1)求在甲學校的50名學生中隨機選擇1名同學,求其視力情況為良好的概率;
(2)根據表1,表2,對在學校推廣眼保健操的必要性進行分析;
(3)在乙學校視力情況一般的學生中選擇2人,了解其具體用眼習慣,求這兩人視力情況都為0.8的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
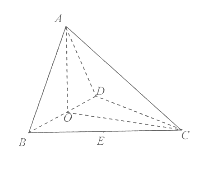
【題目】如圖,四面體ABCD中,O、E分別是BD、BC的中點,![]() ,
,![]() .
.
(1)求證:![]() 平面BCD;
平面BCD;
(2)求異面直線AB與CD所成角的余弦值;
(3)求點E到平面ACD的距離。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com