
分析 ①,函數y=|x|與函數y=($\sqrt{x}$)2定義域不同,不是同一個函數;
②,奇函數y=$\frac{1}{x}$的圖象不通過直角坐標系的原點;
③,根據函數圖象平移原則判定;
④,根據對數運算性質判定.
解答 解:對于①,函數y=|x|與函數y=($\sqrt{x}$)2定義域不同,不是同一個函數,故錯;
對于②,奇函數y=$\frac{1}{x}$的圖象不通過直角坐標系的原點,故錯;
對于③,函數y=3(x-1)2的圖象可由y=3x2的圖象向右平移1個單位得到,正確;
對于④,根據對數運算性質logamn=nlogam(a>0且a≠1,m>0,n∈R)正確.
故答案為:③④
點評 本題考查了命題真假的判定,涉及到了函數的性質,屬于基礎題.


 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
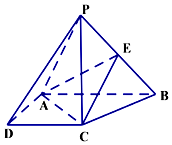 如圖,在四棱錐P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中點.
如圖,在四棱錐P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 0個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若 $α≠\frac{π}{4}$,則tanα≠1 | B. | 若 $α=\frac{π}{4}$,則tanα≠1 | ||
| C. | 若 tanα≠1,則$α≠\frac{π}{4}$ | D. | 若 tanα≠1,則$α=\frac{π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $y=3sin(2x-\frac{π}{6})$ | B. | y=3cos2x | C. | $y=3sin(2x+\frac{π}{3})$ | D. | y=3sin2x |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 銳角三角形 | B. | 直角三角形 | C. | 鈍角三角形 | D. | 等邊三角形 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com