
【題目】已知二次函數![]() 的圖象過點
的圖象過點![]() ,且
,且![]() .
.
(1)求![]() 的解析式;
的解析式;
設數列![]() 滿足
滿足![]() ,求數列
,求數列![]() 的前
的前![]() 項和.
項和.
【答案】(1) ![]() (2)
(2) ![]()
【解析】試題分析:(1)由![]() 列出關于
列出關于![]() 的方程組,,即可解得
的方程組,,即可解得![]() 的值,從而可求出
的值,從而可求出![]() 的解析式;(2)由(1)知
的解析式;(2)由(1)知![]() ,所以可得
,所以可得![]() ,利用錯位相減法結合等比數列求和公式,即可求數列
,利用錯位相減法結合等比數列求和公式,即可求數列![]() 的前
的前![]() 項和.
項和.
試題解析:(1)由![]() ,∴
,∴![]()
解之得![]() ,即
,即![]() .
.
(2)![]()
設![]()
所以![]()
兩式相減![]()
![]()
∴![]()
【 方法點睛】本題主要考查導數的幾何意義、等比數列的求和公式以及錯位相減法求數列的的前![]() 項和,屬于中檔題.一般地,如果數列
項和,屬于中檔題.一般地,如果數列![]() 是等差數列,
是等差數列, ![]() 是等比數列,求數列
是等比數列,求數列![]() 的前
的前![]() 項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列
項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列![]() 的公比,然后作差求解, 在寫出“
的公比,然后作差求解, 在寫出“![]() ”與“
”與“![]() ” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“
” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“![]() ”的表達式.
”的表達式.


科目:高中數學 來源: 題型:
【題目】在對人們休閑方式的一次調查中,共調查120人,其中女性70人,男性50人.女性中有40人主要的休閑方式是看電視,另外30人主要的休閑方式是運動;男性中有20人主要的休閑方式是看電視,另外30人主要的休閑方式是運動.
(1)根據以上數據建立一個2×的列聯表:
休閑方式 性別 | 看電視 | 運 動 | 總 計 |
女 性 | |||
男 性 | |||
總 計 |
(2)有多大的把握認為休閑方式與性別有關?
參考公式及數據:K2=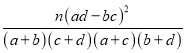
①當K2>2.706時,有90%的把握認為A、B有關聯;
②當K2>3.841時,有95%的把握認為A、B有關聯;
③當K2>6.635時,有99%的把握認為A、B有關聯.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某購物網站對在7座城市的線下體驗店的廣告費指出![]() (萬元)和銷售額
(萬元)和銷售額![]() (萬元)的數據統計如下表:
(萬元)的數據統計如下表:
城市 |
|
|
|
|
|
|
|
廣告費支出 |
|
|
|
|
|
|
|
銷售額 |
|
|
|
|
|
|
|
(Ⅰ)若用線性回歸模型擬合![]() 與
與![]() 關系,求
關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(Ⅱ)若用對數函數回歸模型擬合![]() 與
與![]() 的關系,可得回歸方程
的關系,可得回歸方程![]() ,經計算對數函數回歸模型的相關系數約為
,經計算對數函數回歸模型的相關系數約為![]() ,請說明選擇哪個回歸模型更合適,并用此模型預測
,請說明選擇哪個回歸模型更合適,并用此模型預測![]() 城市的廣告費用支出
城市的廣告費用支出![]() 萬元時的銷售額.
萬元時的銷售額.
參考數據: ![]() ,
, ![]() ,
, ![]() ,
, 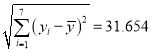 ,
, ![]() ,
, ![]() .
.
參考公式: 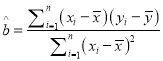 ,
, ![]() .
.
相關系數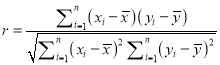 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了治理大氣污染,某市2017年初采用了一系列措施,比如“煤改電”,“煤改氣”,“國Ⅰ,Ⅱ輕型汽油車限行”,“整治散亂污染企業”等.下表是該市2016年和2017年12月份的空氣質量指數(AQI)(AQI指數越小,空氣質量越好)統計表.
表1:2016年12月AQI指數表:單位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 47 | 123 | 232 | 291 | 78 | 103 | 159 | 132 | 37 | 67 | 204 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 270 | 78 | 40 | 51 | 135 | 229 | 270 | 265 | 409 | 429 | 151 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 47 | 155 | 191 | 64 | 54 | 85 | 75 | 249 | 329 |
表2:2017年12月AQI指數表:單位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 91 | 187 | 79 | 28 | 44 | 49 | 27 | 41 | 56 | 43 | 28 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 28 | 49 | 94 | 62 | 40 | 46 | 48 | 55 | 44 | 74 | 62 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 50 | 50 | 46 | 41 | 101 | 140 | 221 | 157 | 55 |
根據表中數據回答下列問題:
(Ⅰ)求出2017年12月的空氣質量指數的極差;
(Ⅱ)根據《環境空氣質量指數(AQI)技術規定(試行)》規定:當空氣質量指數為0~50時,空氣質量級別為一級.從2017年12月12日到12月16這五天中,隨機抽取三天,空氣質量級別為一級的天數為![]() ,求
,求![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅲ)你認為該市2017年初開始采取的這些大氣污染治理措施是否有效?結合數據說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某次有600人參加的數學測試,其成績的頻數分布表如圖所示,規定85分及其以上為優秀.
區間 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人數 | 36 | 114 | 244 | 156 | 50 |
(Ⅰ)現用分層抽樣的方法從這600人中抽取20人進行成績分析,求其中成績為優秀的學生人數;
(Ⅱ)在(Ⅰ)中抽取的20名學生中,要隨機選取2名學生參加活動,記“其中成績為優秀的人數”為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com