
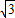 BC-AC 的最大值是( )
BC-AC 的最大值是( )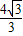
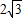
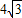
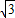 BC-AC=
BC-AC=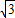 •4sinA-4sinB=4sin(A-30°),再根據-30°<A-30°<120°,可得4sin(A-30°)的最大值.
•4sinA-4sinB=4sin(A-30°),再根據-30°<A-30°<120°,可得4sin(A-30°)的最大值.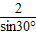 =
=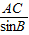 =
= =4,
=4,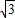 BC-AC=
BC-AC= •4sinA-4sinB=8(
•4sinA-4sinB=8(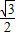 sinA-
sinA- sinB)=8[
sinB)=8[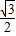 sinA-
sinA- sin(150°-A)]=4[
sin(150°-A)]=4[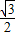 sinA-
sinA- cosA]=4sin(A-30°).
cosA]=4sin(A-30°).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com