
如圖一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。將△ABD沿邊AB折起, 使得△ABD與△ABC成30o的二面角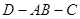 ,如圖二,在二面角
,如圖二,在二面角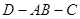 中.
中.
(1) 求CD與面ABC所成的角正弦值的大小;
(2) 對于AD上任意點(diǎn)H,CH是否與面ABD垂直。
(1) 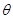 =
= ;
;
(2) CH不可能同時垂直BD和BA,即CH不與面ABD垂直。
解析試題分析:依題意,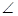 ABD=90o,建立如圖的坐標(biāo)系使得△ABC在yoz平面上,
ABD=90o,建立如圖的坐標(biāo)系使得△ABC在yoz平面上, △ABD與△ABC成30o的二面角,
△ABD與△ABC成30o的二面角, 
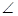 DBY=30o,又AB=BD=2,
DBY=30o,又AB=BD=2,  A(0,0,2),B(0,0,0),C(0,
A(0,0,2),B(0,0,0),C(0,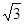 ,1),D(1,
,1),D(1,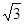 ,0),
,0),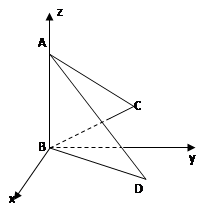
(1) x軸與面ABC垂直,故(1,0,0)是面ABC的一個法向量。
x軸與面ABC垂直,故(1,0,0)是面ABC的一個法向量。
設(shè)CD與面ABC成的角為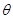 ,而
,而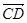 = (1,0,-1),
= (1,0,-1), sin
sin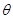 =
=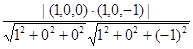 =
=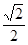

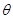
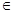 [0,
[0,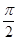 ],
],
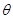 =
= ; 6分
; 6分
(2) 設(shè) =t
=t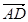 = t(1,
= t(1,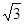 ,-2)= (t,
,-2)= (t,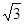 t,-2 t),
t,-2 t),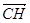 =
= +
+ =(0,-
=(0,-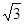 ,1) +(t,
,1) +(t,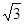 t,-2 t) = (t,
t,-2 t) = (t,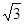 t-
t-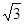 ,-2 t+1),
,-2 t+1),
若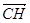
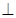
 ,則 (t,
,則 (t,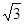 t-
t-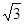 ,-2 t+1)·(0,0,2)="0" 得t=
,-2 t+1)·(0,0,2)="0" 得t=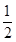 , 10分
, 10分
此時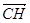 =(
=(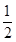 ,-
,-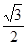 ,0),而
,0),而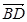 =(1,
=(1,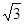 ,0),
,0),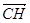 ·
·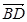 =
=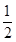 -
-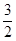 =-1
=-1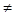 0,
0,
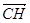 和
和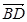 不垂直,即CH不可能同時垂直BD和BA,即CH不與面ABD垂直。12分
不垂直,即CH不可能同時垂直BD和BA,即CH不與面ABD垂直。12分
考點(diǎn):立體幾何中的平行關(guān)系、垂直關(guān)系,角的計算,空間向量的應(yīng)用。
點(diǎn)評:典型題,立體幾何題,是高考必考內(nèi)容,往往涉及垂直關(guān)系、平行關(guān)系、角、距離、體積的計算。在計算問題中,有“幾何法”和“向量法”。利用幾何法,要遵循“一作、二證、三計算”的步驟,本題利用空間向量,簡化了證明及計算過程。



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在幾何體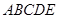 中,
中, 平面
平面 ,
,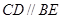 ,
,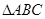 是等腰直角三角形,
是等腰直角三角形,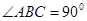 ,且
,且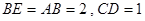 ,點(diǎn)
,點(diǎn) 是
是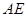 的中點(diǎn).
的中點(diǎn).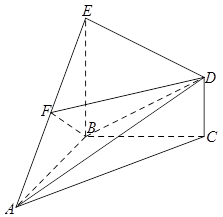
(Ⅰ)求證: 平面
平面 ;
;
(Ⅱ)求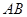 與平面
與平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,四棱錐F-ABCD的底面ABCD是菱形,其對角線AC=2,BD= ,AE、CF都與平面ABCD垂直,AE=1,CF=2.
,AE、CF都與平面ABCD垂直,AE=1,CF=2.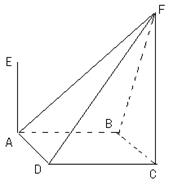
(I)求二面角B-AF-D的大小;
(II)求四棱錐E-ABCD與四棱錐F-ABCD公共部分的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。將△ABD沿邊AB折起, 使得△ABD與△ABC成30o的二面角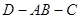 ,如圖二,在二面角
,如圖二,在二面角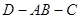 中.
中.
(1) 求CD與面ABC所成的角正弦值的大小;
(2) 對于AD上任意點(diǎn)H,CH是否與面ABD垂直。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O為底面中心, A1O⊥平面ABCD, 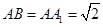 .
. 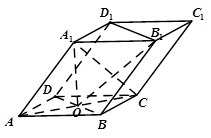
(Ⅰ) 證明: A1C⊥平面BB1D1D;
(Ⅱ) 求平面OCB1與平面BB1D1D的夾角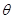 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在等腰梯形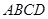 中,
中,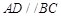 ,
,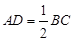 ,
,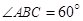 ,
, 是
是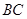 的中點(diǎn).將梯形
的中點(diǎn).將梯形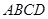 繞
繞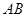 旋轉(zhuǎn)
旋轉(zhuǎn)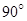 ,得到梯形
,得到梯形 (如圖).
(如圖).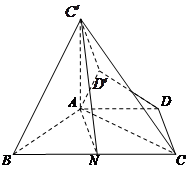
(1)求證: 平面
平面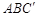 ;
;
(2)求證: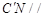 平面
平面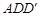 ;
;
(3)求二面角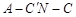 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在四棱錐ABCD-PGFE中,底面ABCD是直角梯形,側(cè)棱垂直于底面,AB//DC,∠ABC=45o,DC=1,AB=2,PA=1.
(Ⅰ)求PD與BC所成角的大小;
(Ⅱ)求證:BC⊥平面PAC;
(Ⅲ)求二面角A-PC-D的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在直角梯形ABCD中,AD//BC,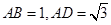 ,
,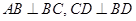 ,如圖(1).把
,如圖(1).把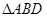 沿
沿 翻折,使得平面
翻折,使得平面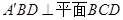 ,如圖(2).
,如圖(2).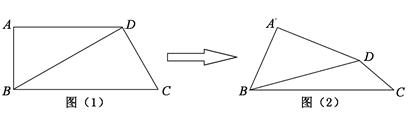
(Ⅰ)求證: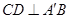 ;
;
(Ⅱ)求三棱錐 的體積;
的體積;
(Ⅲ)在線段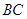 上是否存在點(diǎn)N,使得
上是否存在點(diǎn)N,使得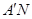
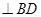 ?若存在,請求出
?若存在,請求出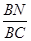 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
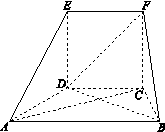
在如圖所示的幾何體中,面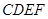 為正方形,面
為正方形,面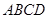 為等腰梯形,
為等腰梯形,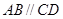 ,
,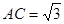 ,
,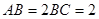 ,
,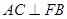 .
.
(1)求證: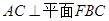 ;
;
(2)求三棱錐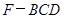 的體積;
的體積;
(3)線段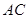 上是否存在點(diǎn)
上是否存在點(diǎn)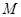 ,使
,使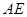 //平面
//平面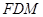 ?證明你的結(jié)論.
?證明你的結(jié)論.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com