
【題目】集合A是由滿足以下性質的函數f(x)組成的:對于任意x≥0,f(x) ∈[-2,4]且f(x)在[0,+∞)上是增函數.
(Ⅰ)試判斷![]() 與
與![]() (x≥0)是否屬于集合A,并說明理由;
(x≥0)是否屬于集合A,并說明理由;
(Ⅱ)對于(Ⅰ)中你認為屬于集合A的函數f(x),證明:對于任意的x≥0,都有f(x)+f(x+2)<2f(x+1).
【答案】(1) ![]() ,
, ![]() (2)見解析.
(2)見解析.
【解析】試題分析:(I)由已知可得函數![]() 的值域
的值域![]() ,從而可得
,從而可得![]() ,對于
,對于![]() ,只要分別判斷函數定義域是否滿足條件①,值域是否滿足條件②,單調性是否滿足條件③,即可得答案;(II)由(I)知,
,只要分別判斷函數定義域是否滿足條件①,值域是否滿足條件②,單調性是否滿足條件③,即可得答案;(II)由(I)知, ![]() 屬于集合
屬于集合![]() ,原不等式為
,原不等式為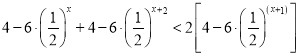 ,利用作差法指數冪的運算法則化簡整理可以證明結論.
,利用作差法指數冪的運算法則化簡整理可以證明結論.
試題解析:(Ⅰ) ![]() ,
, ![]() ,理由如下:
,理由如下:
由于![]() (49)=5>4,
(49)=5>4, ![]() (49)
(49)![]() [-2,4],所以
[-2,4],所以![]() (x)
(x)![]() A.
A.
對于![]()
因為![]() 在[0,+∞)上是減函數,且其值域為(0,1],
在[0,+∞)上是減函數,且其值域為(0,1],
所以![]() 在區間[0,+∞)上是增函數.
在區間[0,+∞)上是增函數.
所以![]() ≥f(0)=-2,且
≥f(0)=-2,且![]() =
=![]() <4,
<4,
所以對于任意x≥0,f(x)∈[-2,4].
所以![]() ∈A
∈A
(Ⅱ)由(Ⅰ)得: ![]() ,
,
f(x+1)=4-![]() =4-3·
=4-3·![]() ,
,
所以2f(x+1)-[f(x)+f(x+2)]=2[4-3·![]() ]-[4-6·
]-[4-6·![]() +4-
+4-![]() ·
·![]() ]=
]=![]() ·
·![]() >0,
>0,
所以對于任意的x≥0,都有f(x)+f(x+2)<2f(x+1).


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知直線l:x+2y-2=0,試求:
(1)點P(-2,-1)關于直線l的對稱點坐標;
(2)直線![]() 關于直線l對稱的直線l2的方程;
關于直線l對稱的直線l2的方程;
(3)直線l關于點(1,1)對稱的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】端午節小長假期間,張洋與幾位同學從天津乘火車到大連去旅游,若當天從天津到大連的三列火車正點到達的概率分別為0.8,0.7,0.9,假設這三列火車之間是否正點到達互不影響,則這三列火車恰好有兩列正點到達的概率是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣1|﹣|x+1|.
(1)求不等式|f(x)|<1的解集;
(2)若不等式|a|f(x)≥|f(a)|對任意a∈R恒成立,求實數x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·湖南)如下圖,直三棱柱ABC-A1B1C1的底面是邊長為2的正三角形,E、F分別是BC、CC1的中點.
(1)證明:平面AEF⊥平面B1BCC1;
(2)若直線A1C與平面A1ABB1所成的角為45°,求三棱錐F-AEC的體積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com