
【題目】已知函數f(x)=sin2x﹣cos2x﹣2 ![]() sinx cosx(x∈R).
sinx cosx(x∈R).
(Ⅰ)求f( ![]() )的值.
)的值.
(Ⅱ)求f(x)的最小正周期及單調遞增區間.
【答案】解:∵函數f(x)=sin2x﹣cos2x﹣2 ![]() sinx cosx=﹣
sinx cosx=﹣ ![]() sin2x﹣cos2x=2sin(2x+
sin2x﹣cos2x=2sin(2x+ ![]() )
)
(Ⅰ)f( ![]() )=2sin(2×
)=2sin(2× ![]() +
+ ![]() )=2sin
)=2sin ![]() =2,
=2,
(Ⅱ)∵ω=2,故T=π,
即f(x)的最小正周期為π,
由2x+ ![]() ∈[﹣
∈[﹣ ![]() +2kπ,
+2kπ, ![]() +2kπ],k∈Z得:
+2kπ],k∈Z得:
x∈[﹣ ![]() +kπ,﹣
+kπ,﹣ ![]() +kπ],k∈Z,
+kπ],k∈Z,
故f(x)的單調遞增區間為[﹣ ![]() +kπ,﹣
+kπ,﹣ ![]() +kπ],k∈Z.
+kπ],k∈Z.
【解析】利用二倍角公式及輔助角公式化簡函數的解析式,
(Ⅰ)代入可得:f( ![]() )的值.
)的值.
(Ⅱ)根據正弦型函數的圖象和性質,可得f(x)的最小正周期及單調遞增區間
【考點精析】通過靈活運用復合函數單調性的判斷方法和正弦函數的單調性,掌握復合函數f[g(x)]的單調性與構成它的函數u=g(x),y=f(u)的單調性密切相關,其規律:“同增異減”;正弦函數的單調性:在![]()
![]() 上是增函數;在
上是增函數;在![]()
![]() 上是減函數即可以解答此題.
上是減函數即可以解答此題.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=1﹣ax+lnx,(x>0),函數g(x)滿足g(x)=x﹣1,(x∈R).
(1)若函數f(x)在x=1時存在極值,求a的值;
(2)在(1)的條件下,當x>1時,blnx< ![]() ,求實數b的取值范圍.
,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() cos(2x﹣
cos(2x﹣ ![]() )﹣2sinxcosx.(13分)
)﹣2sinxcosx.(13分)
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求證:當x∈[﹣ ![]() ,
, ![]() ]時,f(x)≥﹣
]時,f(x)≥﹣ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l、m,平面α、β,下列命題正確的是 ( )
A. l∥β,lαα∥β
B. l∥β,m∥β,lα,mαα∥β
C. l∥m,lα,mβα∥β
D. l∥β,m∥β,lα,mα,l∩m=Mα∥β
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線x2=y,點A(﹣ ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ),拋物線上的點P(x,y)(﹣
),拋物線上的點P(x,y)(﹣ ![]() <x<
<x< ![]() ),過點B作直線AP的垂線,垂足為Q.
),過點B作直線AP的垂線,垂足為Q.
(Ⅰ)求直線AP斜率的取值范圍;
(Ⅱ)求|PA||PQ|的最大值.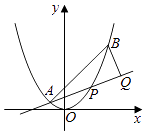
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知空間中三點A(-2,0,2),B(-1,1,2),C(-3,0,4),設a=![]() ,b=
,b=![]() .
.
(1)求向量a與向量b的夾角的余弦值;
(2)若ka+b與ka-2b互相垂直,求實數k的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為ρcosθ=4.
(Ⅰ)M為曲線C1上的動點,點P在線段OM上,且滿足|OM||OP|=16,求點P的軌跡C2的直角坐標方程;
(Ⅱ)設點A的極坐標為(2, ![]() ),點B在曲線C2上,求△OAB面積的最大值.
),點B在曲線C2上,求△OAB面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com