日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
已知橢圓C的方程為+=1,試確定m的取值范圍，使得對一直線y=4x+m,橢圓C上有不同兩點P、Q關于該直線對稱.

思路解析：本題解法很多，可以由Δ判定，也可以由交軌法，還可以考慮設而不求.

解法一：設出對稱的兩點的坐標及其所在的直線方程，再利用判別式Δ＞0及中心在對稱軸上來求解.

設橢圓C上關于直線l對稱的兩點為P（x1,y1）、Q(x2,y2),其所在直線方程為y=-x+b,代入橢圓方程3x2+4y2=12,整理得13x2-8bx+16b2-48=0.

∵x1≠x2,∴Δ=-192(4b2-13)＞0,解得-＜b＜.                          ①

又∵=,=-,+b=b,

而點（,）在直線y=4x+m上，

∴m=-4·=-b.∴b=-m.                                     ②

將②代入①可解得-＜m＜,

即所求m的范圍內（-,）.

解法二：根據中點M必在P、Q兩點之間，建立不等式，將問題轉化為求解直線y=4x+m和過P、Q兩點所在的直線的交點問題.

設PQ中點坐標為M（x0,y0）.

由解法一知，2x0=x1+x2=,x1x2=,

由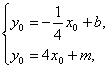消去y0，把x0=b代入可得m=-b,∴x0=-m.

由于中點M的位置（介于P、Q）之間必有不等關系（x1-x0）(x2-x0)＜0,由此可得-＜m＜.

經驗證，當-＜m＜時，

-＜b＜.

適合條件的點P、Q存在.

∴-＜m＜.

解法三：聯想與弦的中點有關，利用“設而不求”法，可轉化為利用均值不等式求出m的范圍.

設P(x1,y1),Q(x2,y2),

若P、Q關于直線l:y=4x+m對稱，當且僅當下列條件組成立.

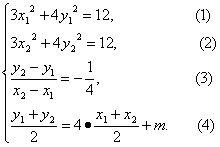
（1）-（2）并把（3）代入,得y1+y2=3(x1+x2).                                              （5）

把（5）代入（4）,得x1+x2=-2m.                                                            （6）

把（6）代入（5）,得y1+y2=-6m.                                                             （7）

①+②,得3（x12+x22）+4(y12+y22)=24.                                       （8）

由題意x1≠x2,y1≠y2,根據均值不等式有

x12+x22＞,y12+y22＞.

∴3(x12+x22)+4(y12+y22)＞ (x1+x2)2+2(y1+y2)2.                 （9）

把（6）（7）（8）代入（9），解得-＜m＜,

即m∈(-,).

解法四：C上存在不同的兩點關于直線l對稱，等價于存在C的弦被l垂直平分，且垂足必在橢圓C的內部，因此，這類問題可轉化為利用交點在曲線C內部建立不等式.

設P(x1,y1),Q(x2,y2),PQ中點M（x0,y0），代入橢圓方程有

3x12+4y12=12,           ①       3x22+4y22=12,           ②

①-②得=-=-=-.                    ③

又y0=4x0+m,                                                                 ④

由③④解得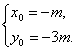

∵M(-m,-3m)在橢圓的內部，

∴3（-m）2+4(-3m)2＜12,解得-＜m＜.

即m∈(-,).

解法五：利用C上存在不同的兩點P、Q關于直線l對稱，則線段PQ中點必在l上，也必在橢圓C的斜率為-的平行弦的中點軌跡上，把問題整體轉化為求橢圓C的斜率為-的平行弦中點的軌跡與直線l交點在橢圓C內部時的參數的取值范圍問題.

設A(x1,y1)、B(x2,y2)是橢圓上的點，且kAB=-,M(x,y)是AB的中點，則有

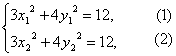
（1）-（2）,得3（x1-x2）(x1+x2)+4(y1-y2)(y1+y2)=0.

∴3x+4y=0,即3x+4y·(-)=0,∴y=3x.

∴橢圓C的斜率為-的平行弦中點軌跡是y=3x在橢圓C內的部分.

由得交點（-m,-3m）.

∵交點在橢圓C內，∴3（-m）2+4(-3m)2＜12.

解得-＜m＜.


練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

已知橢圓C的方程為
x2
a2
+
y2
b2
=1(a≥2b＞0)．
（1）求橢圓C的離心率的取值范圍；
（2）若橢圓C與橢圓2x2+5y2=50有相同的焦點，且過點M（4，1），求橢圓C的標準方程．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知橢圓C的方程為
x2
a2
+ 
y2
b2
=1（a＞b＞0），稱圓心在坐標原點O，半徑為
a2+b2
的圓為橢圓C的“伴隨圓”，橢圓C的短軸長為2，離心率為
6
3
．
（Ⅰ）求橢圓C及其“伴隨圓”的方程；
（Ⅱ）若直線l與橢圓C交于A，B兩點，與其“伴隨圓”交于C，D兩點，當|CD|=
13
 時，求△AOB面積的最大值．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2012•泉州模擬）已知橢圓C的方程為：
x2
a2
+
y2
2
=1 (a＞0)，其焦點在x軸上，離心率e=
2
2
．
（1）求該橢圓的標準方程；
（2）設動點P（x0，y0）滿足
OP
=
OM
+2
ON
，其中M，N是橢圓C上的點，直線OM與ON的斜率之積為-
1
2
，求證：x02+2
y
2
0
為定值．
（3）在（2）的條件下，問：是否存在兩個定點A，B，使得|PA|+|PB|為定值？若存在，給出證明；若不存在，請說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2012•衡陽模擬）已知橢圓C的方程為
y2
a2
+
x2
b2
=1（a＞b＞0），離心率e=
2
2
，上焦點到直線y=
a2
c
的距離為
2
2
，直線l與y軸交于一點P（0，m），與橢圓C交于相異兩點A，B且
AP
=t
PB
．
（1）求橢圓C的方程；
（2）若
OA
+t
OB
=4
OP
，求m的取值范圍•

查看答案和解析>>

科目：高中數學 來源： 題型：

已知橢圓C的方程為
x 2
4
+
y2
3
=1，過C的右焦點F的直線與C相交于A、B兩點，向量
m
=(-1，-4)，若向量
OA
-
OB
與
m
-
OF
共線，則直線AB的方程是（　　）

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 国产99页 | 在线不卡日本 | 亚洲成人高清 | 一级黄色录像视频 | 成人国产精品一级毛片视频 | 国产精品久久国产精品 | 日韩欧美一区二区三区免费观看 | 久久网站热最新地址 | 91色在线 | 男女免费在线观看 | 九九热这里有精品 | 国产日韩欧美 | 日日日操| 一区二区三区在线播放视频 | 色欧美片视频在线观看 | 中文字幕 在线观看 | 成人精品在线视频 | 中文字幕亚洲第一 | 无毒黄网 | 久久激情网| 精品一区二区三区在线视频 | 一级视频黄色 | 日本午夜电影 | 91精品国产自产精品男人的天堂 | 久草 在线 | 久久久久国产一区二区三区四区 | 自拍偷拍第一页 | 操久久| 日韩精品视频在线观看免费 | 在线一区| 9999国产精品 | 夜久久| 国产成人影院 | 久草免费在线 | 嫩草午夜少妇在线影视 | 日韩性xxx | 久久久国产一区二区三区四区小说 | 欧美日韩精品免费 | 久久福利 | 亚洲国产成人精品女人久久久 | 国产精品久久久久久久久久东京 |