
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,且
是正方形,且![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 是線段
是線段![]() 上的一個動點(diǎn).
上的一個動點(diǎn).
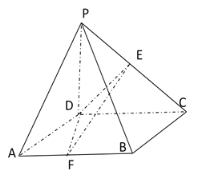
(Ⅰ)求證:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)當(dāng)點(diǎn)![]() 是線段
是線段![]() 上的中點(diǎn)時,求二面角
上的中點(diǎn)時,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(Ⅰ)證明見解析;(Ⅱ)![]()
【解析】
(Ⅰ)推導(dǎo)出![]() 和
和![]() 即可證明
即可證明![]() 平面
平面![]() ,再利用面面垂直判定即可
,再利用面面垂直判定即可
(Ⅱ)以![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,建立如圖所示空間直角坐標(biāo)系
軸,建立如圖所示空間直角坐標(biāo)系![]() ,求得兩個平面的法向量,再利用二面角向量公式求解
,求得兩個平面的法向量,再利用二面角向量公式求解
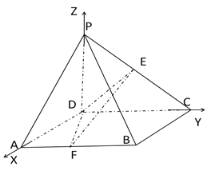
(Ⅰ)證明:∵四邊形![]() 是正方形,∴
是正方形,∴![]() .
.
∵平面![]()
![]() 平面
平面![]() 平面
平面![]()
![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 的中點(diǎn),∴
的中點(diǎn),∴![]() .
.
又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]()
![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)知![]() 平面
平面![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∴![]() ,
,![]() 又
又![]() ,
,
∴![]() ,
,![]() ,
,![]() 兩兩垂直,以
兩兩垂直,以![]() 為原點(diǎn),
為原點(diǎn),
以![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,建立如圖所示空間直角坐標(biāo)系
軸,建立如圖所示空間直角坐標(biāo)系![]() .
.
因為![]() ,∵
,∵![]() .
.
![]() ,
,![]() ,
,![]() ,
,
又![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,
![]()
![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則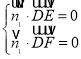 ,
,
∴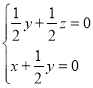 ,令
,令![]() ,則
,則![]() ,
,
∴![]() ,則
,則![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一個法向量
的一個法向量![]() ,
,
![]() .
.
由圖知二面角![]() 的平面角為銳角,則二面角
的平面角為銳角,則二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,兩焦點(diǎn)與短軸的一個端點(diǎn)的連線構(gòu)成的三角形面積為
,兩焦點(diǎn)與短軸的一個端點(diǎn)的連線構(gòu)成的三角形面積為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設(shè)與圓O:![]() 相切的直線l交橢圓C于A,B兩點(diǎn)(O為坐標(biāo)原點(diǎn)),求△AOB面積的最大值。
相切的直線l交橢圓C于A,B兩點(diǎn)(O為坐標(biāo)原點(diǎn)),求△AOB面積的最大值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的圖象在點(diǎn)
的圖象在點(diǎn)![]() 處的切線為
處的切線為![]() ,若函數(shù)
,若函數(shù)![]() 滿足
滿足![]() (其中
(其中![]() 為函數(shù)
為函數(shù)![]() 的定義域,當(dāng)
的定義域,當(dāng)![]() 時,
時,![]() 恒成立,則稱
恒成立,則稱![]() 為函數(shù)
為函數(shù)![]() 的“轉(zhuǎn)折點(diǎn)”,已知函數(shù)
的“轉(zhuǎn)折點(diǎn)”,已知函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在一個“轉(zhuǎn)折點(diǎn)”,則
上存在一個“轉(zhuǎn)折點(diǎn)”,則![]() 的取值范圍是
的取值范圍是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某餅屋進(jìn)行為期![]() 天的五周年店慶活動,現(xiàn)策劃兩項有獎促銷活動,活動一:店慶期間每位顧客一次性消費(fèi)滿
天的五周年店慶活動,現(xiàn)策劃兩項有獎促銷活動,活動一:店慶期間每位顧客一次性消費(fèi)滿![]() 元,可得
元,可得![]() 元代金券一張;活動二:活動期間每位顧客每天有一次機(jī)會獲得一個一元或兩元紅包.根據(jù)前一年該店的銷售情況,統(tǒng)計了
元代金券一張;活動二:活動期間每位顧客每天有一次機(jī)會獲得一個一元或兩元紅包.根據(jù)前一年該店的銷售情況,統(tǒng)計了![]() 位顧客一次性消費(fèi)的金額數(shù)(元),頻數(shù)分布表如下圖所示:
位顧客一次性消費(fèi)的金額數(shù)(元),頻數(shù)分布表如下圖所示:
一次性消費(fèi)金額數(shù) |
|
|
|
|
|
人數(shù) |
|
|
|
|
|
以這![]() 位顧客一次消費(fèi)金額數(shù)的頻率分布代替每位顧客一次消費(fèi)金額數(shù)的概率分布.
位顧客一次消費(fèi)金額數(shù)的頻率分布代替每位顧客一次消費(fèi)金額數(shù)的概率分布.
(1)預(yù)計該店每天的客流量為![]() 人次,求這次店慶期間,商家每天送出代金券金額數(shù)的期望;
人次,求這次店慶期間,商家每天送出代金券金額數(shù)的期望;
(2)假設(shè)顧客獲得一元或兩元紅包的可能性相等,商家在店慶活動結(jié)束后會公布幸運(yùn)數(shù)字,連續(xù)![]() 天參加返紅包的顧客,如果紅包金額總數(shù)與幸運(yùn)數(shù)字一致,則可再獲得
天參加返紅包的顧客,如果紅包金額總數(shù)與幸運(yùn)數(shù)字一致,則可再獲得![]() 元的“店慶幸運(yùn)紅包”一個.若公布的幸運(yùn)數(shù)字是“
元的“店慶幸運(yùn)紅包”一個.若公布的幸運(yùn)數(shù)字是“![]() ”,求店慶期間一位連續(xù)
”,求店慶期間一位連續(xù)![]() 天消費(fèi)的顧客獲得紅包金額總數(shù)的期望.
天消費(fèi)的顧客獲得紅包金額總數(shù)的期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,![]() 平面PCD,
平面PCD,![]() ,
,![]() ,
,![]() ,E為AD的中點(diǎn),AC與BE相交于點(diǎn)O.
,E為AD的中點(diǎn),AC與BE相交于點(diǎn)O.

(1)證明:![]() 平面ABCD.
平面ABCD.
(2)求直線BC與平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,曲線C的參數(shù)方程為![]() (
(![]() 為參數(shù)),以平面直角坐標(biāo)系的原點(diǎn)O為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系.
為參數(shù)),以平面直角坐標(biāo)系的原點(diǎn)O為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系.
(1)求曲線C的極坐標(biāo)方程;
(2)過點(diǎn)![]() ,傾斜角為
,傾斜角為![]() 的直線l與曲線C相交于M,N兩點(diǎn),求
的直線l與曲線C相交于M,N兩點(diǎn),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】人們常說的“幸福感指數(shù)”就是指某個人主觀地評價他對自己目前生活狀態(tài)的滿意程度的指標(biāo),常用區(qū)間![]() 內(nèi)的一個數(shù)來表示,該數(shù)越接近
內(nèi)的一個數(shù)來表示,該數(shù)越接近![]() 表示滿意度越高.為了解某地區(qū)居民的幸福感情況,隨機(jī)對該地區(qū)的男、女居民各
表示滿意度越高.為了解某地區(qū)居民的幸福感情況,隨機(jī)對該地區(qū)的男、女居民各![]() 人進(jìn)行了調(diào)查,調(diào)查數(shù)據(jù)如表所示:
人進(jìn)行了調(diào)查,調(diào)查數(shù)據(jù)如表所示:
幸福感指數(shù) |
|
|
|
|
|
男居民人數(shù) |
|
|
|
|
|
女居民人數(shù) |
|
|
|
|
|
(1)估算該地區(qū)居民幸福感指數(shù)的平均值;
(2)若居民幸福感指數(shù)不小于![]() ,則認(rèn)為其幸福.為了進(jìn)一步了解居民的幸福滿意度,調(diào)查組又在該地區(qū)隨機(jī)抽取
,則認(rèn)為其幸福.為了進(jìn)一步了解居民的幸福滿意度,調(diào)查組又在該地區(qū)隨機(jī)抽取![]() 對夫妻進(jìn)行調(diào)查,用
對夫妻進(jìn)行調(diào)查,用![]() 表示他們之中幸福夫妻(夫妻二人都感到幸福)的對數(shù),求
表示他們之中幸福夫妻(夫妻二人都感到幸福)的對數(shù),求![]() 的期望(以樣本的頻率作為總體的概率).
的期望(以樣本的頻率作為總體的概率).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】世界軍人運(yùn)動會,簡稱“軍運(yùn)會”,是國際軍事體育理事會主辦的全球軍人最高規(guī)格的大型綜合性運(yùn)動會,每四年舉辦一屆,會期7至10天,比賽設(shè)27個大項,參賽規(guī)模約100多個國家8000余人,規(guī)模僅次于奧運(yùn)會,是和平時期各國軍隊展示實(shí)力形象、增進(jìn)友好交流、擴(kuò)大國際影響的重要平臺,被譽(yù)為“軍人奧運(yùn)會”.根據(jù)各方達(dá)成的共識,軍運(yùn)會于2019年10月18日至27日在武漢舉行,賽期10天,共設(shè)置射擊、游泳、田徑、籃球等27個大項、329個小項.其中,空軍五項、軍事五項、海軍五項、定向越野和跳傘5個項目為軍事特色項目,其他項目為奧運(yùn)項目.現(xiàn)對某國在射擊比賽預(yù)賽中的得分?jǐn)?shù)據(jù)進(jìn)行分析,得到如下的頻率分布直方圖:
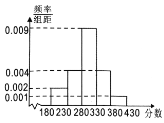
(1)估計某國射擊比賽預(yù)賽成績得分的平均值![]() (同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值代表);
(同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值代表);
(2)根據(jù)大量的射擊成績測試數(shù)據(jù),可以認(rèn)為射擊成績![]() 近似地服從正態(tài)分布
近似地服從正態(tài)分布![]() ,經(jīng)計算第(1)問中樣本標(biāo)準(zhǔn)差
,經(jīng)計算第(1)問中樣本標(biāo)準(zhǔn)差![]() 的近似值為50,用樣本平均數(shù)
的近似值為50,用樣本平均數(shù)![]() 作為
作為![]() 的近似值,用樣本標(biāo)準(zhǔn)差
的近似值,用樣本標(biāo)準(zhǔn)差![]() 作為
作為![]() 的估計值,求射擊成績得分
的估計值,求射擊成績得分![]() 恰在350到400的概率;[參考數(shù)據(jù):若隨機(jī)變量
恰在350到400的概率;[參考數(shù)據(jù):若隨機(jī)變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則:
,則:![]() ,
,![]() ,
,![]() ;
;
(3)某汽車銷售公司在軍運(yùn)會期間推廣一款新能源汽車,現(xiàn)面向意向客戶推出“玩游戲,送大獎”,活動,客戶可根據(jù)拋擲骰子的結(jié)果,操控微型遙控車在方格圖上行進(jìn),若遙控車最終停在“勝利大本營”,則可獲得購車優(yōu)惠券.已知骰子出現(xiàn)任意點(diǎn)數(shù)的概率都是![]() ,方格圖上標(biāo)有第0格,第1格,第2格,……第50格.遙控車開始在第0格,客戶每拋擲一次骰子,遙控車向前移動一次,若拋擲出正面向上的點(diǎn)數(shù)是1,2,3,4,5點(diǎn),遙控車向前移動一格(從
,方格圖上標(biāo)有第0格,第1格,第2格,……第50格.遙控車開始在第0格,客戶每拋擲一次骰子,遙控車向前移動一次,若拋擲出正面向上的點(diǎn)數(shù)是1,2,3,4,5點(diǎn),遙控車向前移動一格(從![]() 到
到![]() ),若拋擲出正面向上的點(diǎn)數(shù)是6點(diǎn),遙控車向前移動兩格(從
),若拋擲出正面向上的點(diǎn)數(shù)是6點(diǎn),遙控車向前移動兩格(從![]() 到
到![]() ),直到遙控車移動到第49格(勝利大本營)或第50格(失敗大本營)時,游戲結(jié)束.設(shè)遙控車移動到第
),直到遙控車移動到第49格(勝利大本營)或第50格(失敗大本營)時,游戲結(jié)束.設(shè)遙控車移動到第![]() 格的概率為
格的概率為![]() ,試證明
,試證明![]() 是等比數(shù)列,并求
是等比數(shù)列,并求![]() ,以及根據(jù)
,以及根據(jù)![]() 的值解釋這種游戲方案對意向客戶是否具有吸引力.
的值解釋這種游戲方案對意向客戶是否具有吸引力.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com