解:(Ⅰ)證明:假設存在x'
0,x
0∈(a,b),且x'
0≠x
0,使得
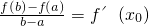
,
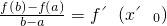
,
即f'(x
0)=f'(x'
0).(1分)
∵
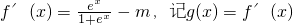
,∴
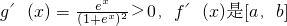
上的單調增函數(或者通過復合函數單調性說明f'(x)的單調性).(3分)
∴x
0=x'
0,這與x'
0≠x
0矛盾,即x
0是唯一的.(4分)
(Ⅱ)

,原因如下:
設

,則
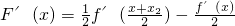
.
由(Ⅰ)知f'(x)單調增.
所以當x>x
2即
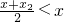
時,有
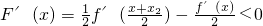
所以x>x
2時,F(x)單調減.(5分)
當x<x
2即
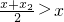
時,有
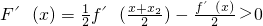
所以x<x
2時,F(x)單調增.(6分)
所以F(x)<F(x
2)=0,所以

.(8分)
(Ⅲ)證明:設A(x
1,y
1),B(x
2,y
2),C(x
3,y
3),且x
1<x
2<x
3,因為m≥1
∵
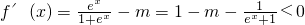
,∴f(x)是x∈R上的單調減函數.(9分)
∴f(x
1)>f(x
2)>f(x
3).∵
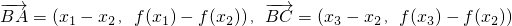
,
∴
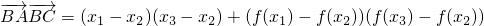
.(10分)
∵x
1-x
2<0,x
3-x
2>0,f(x
1)-f(x
2)>0,f(x
3)-f(x
2)<0,
∴
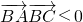
,∴cosB<0,∠B為鈍角.故△ABC為鈍角三角形.(12分)
分析:(Ⅰ)假設存在x'
0,x
0∈(a,b),且x'
0≠x
0,使得f'(x
0)=f'(x'
0),由此導出
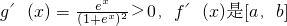
上的單調增函數,從而得到x
0是唯一的.
(Ⅱ)

,設

,則
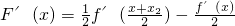
.由f'(x)單調增.知x>x
2時,F(x)單調減.x<x
2時,F(x)單調增,所以

.
(Ⅲ)設A(x
1,y
1),B(x
2,y
2),C(x
3,y
3),且x
1<x
2<x
3,因為m≥1,由
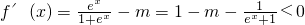
,知f(x)是x∈R上的單調減函數由此入手能推導出△ABC為鈍角三角形.
點評:本題考查利用導數判斷函數的單調性的綜合運用,具有一定的難度,解題時要認真審題,注意題設中的隱含條件,合理地進行等價轉換.

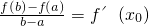 成立,求證:x0唯一;
成立,求證:x0唯一; )和
)和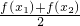 大小,并說明理由;
大小,并說明理由;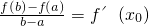 ,
,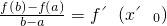 ,
,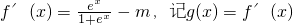 ,∴
,∴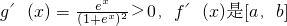 上的單調增函數(或者通過復合函數單調性說明f'(x)的單調性).(3分)
上的單調增函數(或者通過復合函數單調性說明f'(x)的單調性).(3分) ,原因如下:
,原因如下: ,則
,則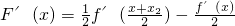 .
.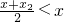 時,有
時,有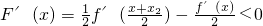
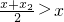 時,有
時,有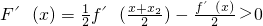
 .(8分)
.(8分)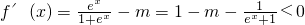 ,∴f(x)是x∈R上的單調減函數.(9分)
,∴f(x)是x∈R上的單調減函數.(9分)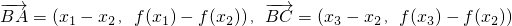 ,
,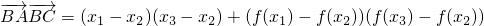 .(10分)
.(10分)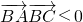 ,∴cosB<0,∠B為鈍角.故△ABC為鈍角三角形.(12分)
,∴cosB<0,∠B為鈍角.故△ABC為鈍角三角形.(12分)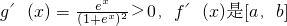 上的單調增函數,從而得到x0是唯一的.
上的單調增函數,從而得到x0是唯一的. ,設
,設 ,則
,則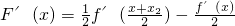 .由f'(x)單調增.知x>x2時,F(x)單調減.x<x2時,F(x)單調增,所以
.由f'(x)單調增.知x>x2時,F(x)單調減.x<x2時,F(x)單調增,所以 .
.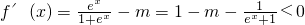 ,知f(x)是x∈R上的單調減函數由此入手能推導出△ABC為鈍角三角形.
,知f(x)是x∈R上的單調減函數由此入手能推導出△ABC為鈍角三角形.

 應用題作業本系列答案
應用題作業本系列答案 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案