如圖,
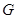
是△
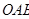
的重心,
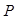
、
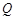
分別是邊
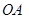
、
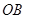
上的動點,且
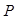
、
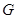
、
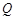
三點共線.
(1)設
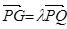
,將
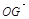
用
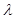
、
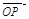
、
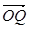
表示;
(2)設
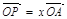
,
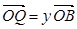
,證明:
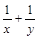
是定值;
(3)記△
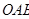
與△
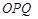
的面積分別為
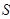
、
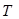
.求
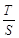
的取值范圍.
(提示:
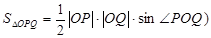
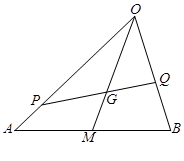
第一問中利用(1)
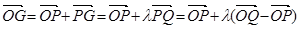
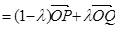
第二問中,由(1),得
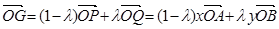
;①
另一方面,∵
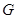
是△
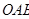
的重心,
∴
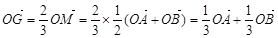
而
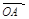
、
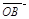
不共線,∴由①、②,得
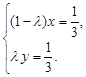
第三問中,
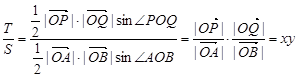
由點
、
的定義知
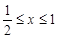
,
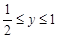
,
且
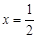
時,
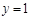
;
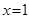
時,
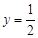
.此時,均有
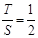
.
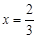
時,
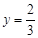
.此時,均有
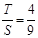
.
以下證明:
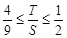
,結合作差法得到。
解:(1)
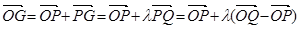
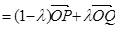
.
(2)一方面,由(1),得
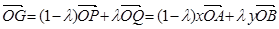
;①
另一方面,∵
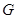
是△
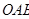
的重心,
∴
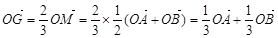
. ②
而
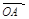
、
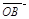
不共線,∴由①、②,得
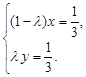
解之,得
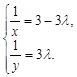
,∴
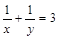
(定值).
(3)
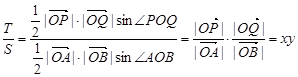
.
由點
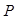
、
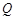
的定義知
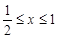
,
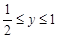
,
且
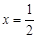
時,
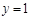
;
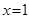
時,
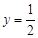
.此時,均有
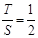
.
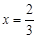
時,
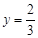
.此時,均有
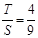
.
以下證明:
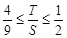
.(法一)由(2)知
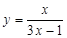
,
∵
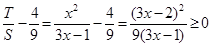
,∴
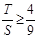
.
∵
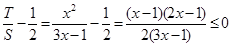
,∴
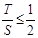
.
∴
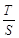
的取值范圍
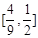
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
已知向量
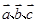
兩兩之間的夾角為60°,其模長都為1,則|
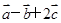
|等于
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題

向量
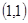
向上向左均平移1個單位后所得向量為 ;
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在△ABC中,
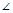
A=90°,AB=1,設點P,Q滿足
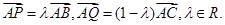
若
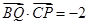
,則
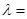
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設
O為坐標原點,點
M坐標為
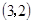
,若點
N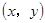
滿足不等式組
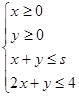
,當
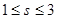
時,則
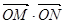
的最大值的變化范圍是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知點G是△ABC的重心,若∠A=120°,
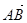
·
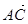
=-2,則|
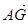
|的最小值是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
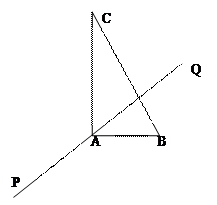
(文)如圖,在Rt△ABC中,已知BC=a,若長為2a的線段PQ以點A為中點,問
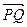
與
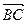
的夾角θ取何值時,
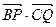
的值最大?并求出這個最大值。

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知A、B、C是圓O:
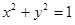
上三點,且
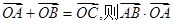
=
.
查看答案和解析>>

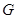 是△
是△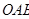 的重心,
的重心,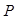 、
、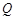 分別是邊
分別是邊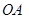 、
、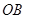 上的動點,且
上的動點,且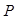 、
、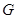 、
、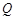 三點共線.
三點共線.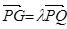 ,將
,將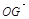 用
用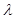 、
、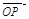 、
、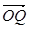 表示;
表示;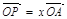 ,
,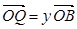 ,證明:
,證明: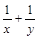 是定值;
是定值;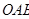 與△
與△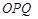 的面積分別為
的面積分別為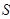 、
、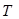 .求
.求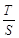 的取值范圍.
的取值范圍.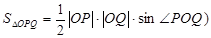
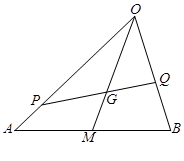
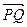 與
與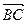 的夾角θ取何值時,
的夾角θ取何值時,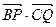 的值最大?并求出這個最大值。
的值最大?并求出這個最大值。
