Question

如圖，正方形ABCD，有一直徑為BC的半圓，BC=2cm，現(xiàn)有兩點E、F，分別從點B、點A同時出發(fā)，點E沿線段BA以1cm/s的速度向點A運動，點F沿折線A-D-C以2 cm/s的速度向點C運動，設E離開點B的時間為t s．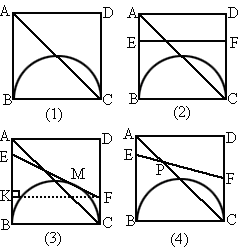

(1)當t為何值時，線段EF與BC平行；

(2)設1＜t＜2，當t為何值時，EF與半圓相切?

(3)當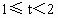時，設EF與AC相交于點P，問點E、F運動時，點P的位置是否發(fā)生變化?若變化，請說明理由；若不變化，請給予證明，并求AP∶PC的值．

Answer 1

答案：略
解析：

解：(1)∵四邊形ABCD為正方形，∴AB∥DC，而EF∥BC，∴BE=FC．∵BE=t，CF=4－2t，∴t=4－2t，得，即當時，線段EF∥BC． (2)設E、F出發(fā)t s時，EF與半圓相切，如圖(3)， ∴EF=EM＋MF=EB＋FC(切線長定理)． 作FK⊥AB，進而KB=FC． 又∵， 于是， 即，解之，得． ∵1＜t＜2，∴， 即當時，EF與半圓相切． (3)當時，點P的位置不會發(fā)生變化． 事實上，設時，E、F出發(fā)t s后的線段位置，如圖(4)， 則， 而由AB∥DC，有△APE∽△CPF， 可知，這個比值顯然與t無關，因而點P的位置不會發(fā)生變化．

提示：

分析：本題是典型的運動幾何問題，用運動變化觀點分析與看待此問題．對于(1)與(2)的解答均是先假設結論成立，逆向思考從而求出t的值．對于(3)討論是否與t有關，可判定點P的位置是否發(fā)生變化．