【答案】
分析:(1)據求導法則求出導函數,代入已知條件得關系.
(2)令導數為0得兩個根,分類討論兩個根大小判斷根左右兩邊導數的符號,得函數單調性.
(3)由(2)求出極值點,由兩點式求出直線方程,與曲線方程聯立判斷有無其他公共點.
解答:解:解法一:(1)依題意,得
f′(x)=x
2+2ax+b.
由f′(-1)=1-2a+b=0得b=2a-1.
(2)由(1)得f(x)=x
3+ax
2+(2a-1)x,故f′(x)=x
2+2ax+2a-1=(x+1)(x+2a-1).
令f′(x)=0,則x=-1或x=1-2a.
①當a>1時,1-2a<-1.
當x變化時,f′(x)與f(x)的變化情況如下表:

由此得,函數f(x)的單調增區間為(-∞,1-2a)和(-1,+∞),單調減區間為(1-2a,-1).
②當a=1時,1-2a=-1.此時,f′(x)≥0恒成立,且僅在x=-1處f′(x)=0,故函數f(x)的單調增區間為R.
③當a<1時,1-2a>-1,同理可得函數f(x)的單調增區間為(-∞,-1)和(1-2a,+∞),單調減區間為(-1,1-2a).
綜上所述:當a>1時,函數f(x)的單調增區間為(-∞,1-2a)和(-1,+∞),單調減區間為(1-2a,-1);
當a=1時,函數f(x)的單調增區間為R;
當a<1時,函數f(x)的單調增區間為(-∞,-1)和(1-2a,+∞),單調減區間為(-1,1-2a).
(3)當a=-1時,得f(x)=

x
3-x
2-3x.
由f′(x)=x
2-2x-3=0,得x
1=-1,x
2=3.
由(2)得f(x)的單調增區間為(-∞,-1)和(3,+∞),單調減區間為(-1,3),
所以函數f(x)在x
1=-1,x
2=3處取得極值.故M(-1,

),N(3,-9).
所以直線MN的方程為y=-

x-1.
由
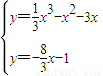
得x
3-3x
2-x+3=0.
令F(x)=x
3-3x
2-x+3.
易得F(0)=3>0,F(2)=-3<0,而F(x)的圖象在(0,2)內是一條連續不斷的曲線,
故F(x)在(0,2)內存在零點x
,這表明線段MN與曲線f(x)有異于M,N的公共點.
解法二:(1)同解法一.
(2)同解法一.
(3)當a=-1時,得f(x)=

x
3-x
2-3x.
由f′(x)=x
2-2x-3=0,得x
1=-1,x
2=3.
由(2)得f(x)的單調增區間為(-∞,-1)和(3,+∞),單調減區間為(-1,3),所以函數f(x)在x
1=-1,x
2=3處取得極值,
故M(-1,

),N(3,-9).
所以直線MN的方程為y=-

x-1.
由x
3-3x
2-x+3=0.
解得x
1=-1,x
2=1,x
3=3.
∴

,
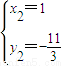
,

所以線段MN與曲線F(x)有異于M,N的公共點(1,-
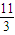
).
點評:本小題主要考查函數、導數等基礎知識,考查推理論證能力、運算求解能力,考查函數與方程思想、數形結合思想、化歸與轉化思想、分類與整合思想.

 x3+ax2+bx,且f′(-1)=0.
x3+ax2+bx,且f′(-1)=0.
 x3-x2-3x.
x3-x2-3x. ),N(3,-9).
),N(3,-9). x-1.
x-1.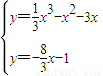 得x3-3x2-x+3=0.
得x3-3x2-x+3=0. x3-x2-3x.
x3-x2-3x. ),N(3,-9).
),N(3,-9). x-1.
x-1. ,
,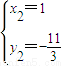 ,
,
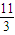 ).
).

 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<