
【題目】已知函數![]() .
.
(Ⅰ)若函數![]() 在定義域上是增函數,求實數
在定義域上是增函數,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若![]() ,令
,令![]() ,試討論函數
,試討論函數![]() 的零點個數,并說明理由.
的零點個數,并說明理由.
【答案】(Ⅰ)![]() .(Ⅱ)見解析
.(Ⅱ)見解析
【解析】試題分析:(1)函數在某區間上為增函數就是要求函數的導數在某區間上非負,求出函數的導數,由于含參,所以對參數分類兩種情況討論,當![]() 時,導數非負恒成立,當
時,導數非負恒成立,當![]() ,導數值有正有負有零,不合題意舍;(2)寫出函數F(x)并求導,分m=1和m>1兩種情況研究,當m=1時,函數單調減,一個零點,當 m>1時,寫出函數的單調區間,圖象先減后增再減,由于極小值為正,只能當極大值小于零時,才會有一個零點,解出m的范圍 .
,導數值有正有負有零,不合題意舍;(2)寫出函數F(x)并求導,分m=1和m>1兩種情況研究,當m=1時,函數單調減,一個零點,當 m>1時,寫出函數的單調區間,圖象先減后增再減,由于極小值為正,只能當極大值小于零時,才會有一個零點,解出m的范圍 .
試題解析:
(Ⅰ)依題意得, ![]() ,
, ![]() ,
,
當![]() 時,
時, ![]() ,故函數
,故函數![]() 在
在![]() 上單調遞增,符合題意;
上單調遞增,符合題意;
當![]() 時,
時, 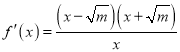 ,
,
令![]() ,得
,得![]() ,函數
,函數![]() 單調遞減,
單調遞減,
令![]() ,得
,得![]() ,函數
,函數![]() 單調遞增,
單調遞增,
故函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,不合題意.
上單調遞增,不合題意.
綜上所述,實數![]() 的取值范圍為
的取值范圍為![]() .
.
(Ⅱ)![]() (
(![]() ),
),
易得![]() .
.
①若![]() ,則
,則![]() ,函數
,函數![]() 為減函數,
為減函數,
注意到![]() ,
, ![]() ,所以
,所以![]() 有唯一零點;
有唯一零點;
②若![]() ,則當
,則當![]() 或
或![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
所以函數![]() 在
在![]() 和
和![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
注意到![]() ,
, ![]() ,所以
,所以![]() 有唯一零點.
有唯一零點.
綜上,當![]() 時,函數
時,函數![]() 有唯一零點.
有唯一零點.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:高中數學 來源: 題型:
【題目】某學校運動會的立定跳遠和30秒跳繩兩個單項比賽分成預賽和決賽兩個階段.下表為10名學生的預賽成績,其中有三個數據模糊.
學生序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳遠(單位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳繩(單位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在這10名學生中,進入立定跳遠決賽的有8人,同時進入立定跳遠決賽和30秒跳繩決賽的有6人,則
(A)2號學生進入30秒跳繩決賽
(B)5號學生進入30秒跳繩決賽
(C)8號學生進入30秒跳繩決賽
(D)9號學生進入30秒跳繩決賽
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以原點為極點,x軸的正半軸為極軸建立極坐標系.已知曲線C:ρsin2θ=2acos θ(a>0),過點P(-2,-4)的直線l的參數方程為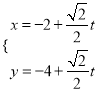 ,直線l與曲線C分別交于M,N兩點.若|PM|,|MN|,|PN|成等比數列,則a的值為________.
,直線l與曲線C分別交于M,N兩點.若|PM|,|MN|,|PN|成等比數列,則a的值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①將一組數據中的每個數據都加上或減去同一個常數后,方差恒不變;
②設有一個回歸方程![]() =3-5x,變量x增加一個單位時,y平均增加5個單位;
=3-5x,變量x增加一個單位時,y平均增加5個單位;
③線性回歸方程![]() =
=![]() x+
x+![]() 必過(
必過(![]() ,
,![]() );
);
④在一個2×2列聯表中,由計算得K2=13.079,則有99%以上的把握認為這兩個變量間有關系.
其中錯誤的個數是( )
本題可以參考獨立性檢驗臨界值表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
A. 0 B. 1
C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016·武昌調研)如圖,在圓內畫1條線段,將圓分成2部分;畫2條相交線段,將圓分割成4部分;畫3條線段,將圓最多分割成7部分;畫4條線段,將圓最多分割成11部分.則
![]()
(1)在圓內畫5條線段,將圓最多分割成________部分;
(2)在圓內畫n條線段,將圓最多分割成________部分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 及圓
及圓![]() .
.
(1)設過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,當
兩點,當![]() 時,求以線段
時,求以線段![]() 為直徑的圓
為直徑的圓![]() 的方程;
的方程;
(2)設直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,是否存在實數
兩點,是否存在實數![]() ,使得過點
,使得過點![]() 的直線
的直線![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出實數
?若存在,求出實數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現需要設計一個倉庫,它由上下兩部分組成,上部的形狀是正四棱錐P—A1B1C1D1,下部的形狀是正四棱柱ABCD—A1B1C1D1(如圖所示),并要求正四棱柱的高O1O是正四棱錐的高PO1的4倍.
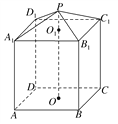
(1)若AB=6 m,PO1=2 m,則倉庫的容積是多少?
(2)若正四棱錐的側棱長為6 m,則當PO1為多少時,倉庫的容積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某山區外圍有兩條相互垂直的直線型公路,為進一步改善山區的交通現狀,計劃修建一條連接兩條公路和山區邊界的直線型公路,記兩條相互垂直的公路為l1,l2,山區邊界曲線為C,計劃修建的公路為l,如圖所示,M,N為C的兩個端點,測得點M到l1,l2的距離分別為5千米和40千米,點N到l1,l2的距離分別為20千米和2.5千米,以l2,l1所在的直線分別為x,y軸,建立平面直角坐標系xOy,假設曲線C符合函數y=![]() (其中a,b為常數)模型.
(其中a,b為常數)模型.
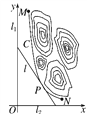
(1)求a,b的值;
(2)設公路l與曲線C相切于P點,P的橫坐標為t.
①請寫出公路l長度的函數解析式f(t),并寫出其定義域;
②當t為何值時,公路l的長度最短?求出最短長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com