某商場預計2014年從1月起前
個月顧客對某種商品的需求總量
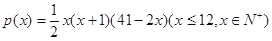（單位：件）
（1）寫出第個月的需求量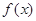
的表達式；
（2）若第個月的銷售量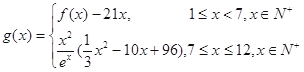
（單位：件），每件利潤
（單位：元），求該商場銷售該商品，預計第幾個月的月利潤達到最大值？月利潤的最大值是多少？（參考數據：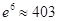
）
(1) f(x)=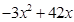 
.
;(2) .第6個月時最大利潤為3000元
解析試題分析：(1)利用數列求和的遞推思想可得第x個月的需求量.
（2）由（1）可得第x個月的需求量.根據利潤計算公式求得月利潤.利用分段函數的范圍求出各段利潤的最大值.最大值的求解是通過求導的知識.本題屬于應用題的問題，閱讀理解題意要細心.其中涉及求和的問題，有涉及第幾個月的問題，及是數列中的通項與求和關系.另外通過分段的求導在對比出最大值.
試題解析：（1）
時，f(x)="p(x)-p(x-1)=" 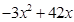.x=1時p(x)=39也滿足所以f(x)= ..
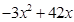(2)設該商場第x個月的月利潤為w（元）.則①
且
時.w(x)= 
.
.由
.得x=6.所以w(x)在[1,6]上遞增，在[6,7)上遞減.所以
.②
且時
=1000
.
.所以w(x)在[7,8]上遞增，在（8,12]上遞減.所以
.綜上.第6個月時最大利潤為3000元.
考點：1.數列的通項問題.2.導數求最值問題.3.分段函數問題.
名校課堂系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，
．
時，求函數
的極小值；
上為增函數，求
的取值范圍．
.
的單調區間；
在區間
上恒成立，求實數
的取值范圍.
.
的單調區間；
上是減函數，求實數a的最小值；
，使
（
）成立，求實數a的取值范圍. 
，
，(其中
)，設
.
時,試將
表示成
的函數
,并探究函數
時，若存在
，使
成立，試求
的范圍.
.
的值域為
，若關于
的不等式
的解集為
，求
的值；
時，
為常數，且
，
，求
的取值范圍.
（
，
），
．
時，對于任意不相等的兩個正實數
、
，均有
成立；
，
在
上單調遞增，求實數
的取值范圍；
.
時，求
的單調區間；
，設
是函數
，記
分別為
，求實數
的取值范圍.
。
的單調區間；
，證明當
時，函數
圖象的上方.