
分析 設出M(3,1)關于直線y=x的對稱點的坐標M0(x0,y0),由兩點的中點在直線y=x上,且兩點連線與直線y=x垂直聯立方程組得答案.
解答 解:設M(3,1)關于直線y=x的對稱點為M0(x0,y0),
則MM0的中點為($\frac{{x}_{0}+3}{2}$,$\frac{{y}_{0}+1}{2}$),
則($\frac{{x}_{0}+3}{2}$,$\frac{{y}_{0}+1}{2}$),
在直線y=x上,
∴$\frac{{x}_{0}+3}{2}$=$\frac{{y}_{0}+1}{2}$,①
再由直線MM0與直線y=x垂直,得$\frac{{y}_{0}-1}{{x}_{0}-3}$=-1 ②
聯立①②解得:x0=1,y0=3.
∴點M(3,1)關于直線y=x的對稱點的坐標是(1,3).
故答案為:(1,3).
點評 本題考查了點關于點的對稱點的求法,體現了數學轉化思想方法,屬中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
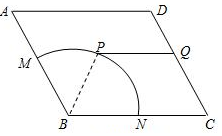 如圖,某廣場中間有一塊邊長為2百米的菱形狀綠化區ABCD,其中BMN是半徑為1百米的扇形,∠ABC=$\frac{2π}{3}$.管理部門欲在該地從M到D修建小路:在$\widehat{MN}$上選一點P(異于M、N兩點),過點P修建與BC平行的小路PQ.
如圖,某廣場中間有一塊邊長為2百米的菱形狀綠化區ABCD,其中BMN是半徑為1百米的扇形,∠ABC=$\frac{2π}{3}$.管理部門欲在該地從M到D修建小路:在$\widehat{MN}$上選一點P(異于M、N兩點),過點P修建與BC平行的小路PQ.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com