
如圖,半徑為30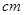 的圓形(
的圓形(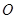 為圓心)鐵皮上截取一塊矩形材料
為圓心)鐵皮上截取一塊矩形材料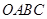 ,其中點
,其中點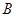 在圓弧上,點
在圓弧上,點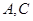 在兩半徑上,現將此矩形材料卷成一個以
在兩半徑上,現將此矩形材料卷成一個以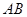 為母線的圓柱形罐子的側面(不計剪裁和拼接損耗),設
為母線的圓柱形罐子的側面(不計剪裁和拼接損耗),設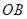 與矩形材料的邊
與矩形材料的邊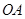 的夾角為
的夾角為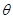 ,圓柱的體積為
,圓柱的體積為
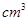 .
.
(Ⅰ)求 關于
關于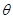 的函數關系式?
的函數關系式?
(Ⅱ)求圓柱形罐子體積 的最大值.
的最大值.
(Ⅰ)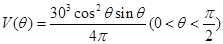 ;(Ⅱ)
;(Ⅱ)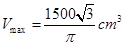 。
。
解析試題分析:方法一:(Ⅰ)在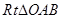 中,
中,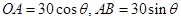 ,將此矩形材料卷成一個以
,將此矩形材料卷成一個以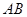 為母線的圓柱,則其底面周長為
為母線的圓柱,則其底面周長為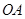 ,設地面半徑為
,設地面半徑為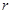 ,則
,則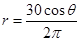 ,由柱體的體積公式,可知
,由柱體的體積公式,可知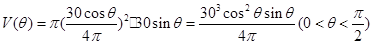 ;(Ⅱ)利用換元法求解,令
;(Ⅱ)利用換元法求解,令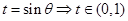 ,則
,則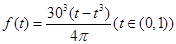 ,對其求導可知函數
,對其求導可知函數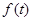 在
在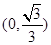 上單調遞增,在
上單調遞增,在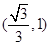 上單調遞減,可知當
上單調遞減,可知當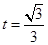 時,體積
時,體積 取得最大值
取得最大值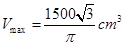 .
.
方法二:(1)連接OB,在Rt△OAB中,由AB=x,則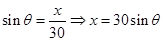 ,利用勾股定理可得
,利用勾股定理可得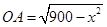 ,設圓柱底面半徑為r,則
,設圓柱底面半徑為r,則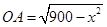 =2πr,即可得出r.
=2πr,即可得出r.
利用V=πr2•x(其中0<x<30)即可得出V與x的關系,進而得到 關于
關于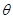 的函數關系式.
的函數關系式.
(2)利用(1)可知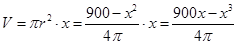 (
(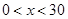 ),再對V求導得V′,得出其單調性,可知
),再對V求導得V′,得出其單調性,可知 在
在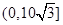 上是增函數,在
上是增函數,在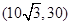 上是減函數,所以當
上是減函數,所以當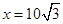 時,
時, 有最大值.
有最大值.
試題解析:【解法1】:(1)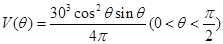
(2)令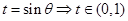 ,
,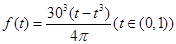 ,
,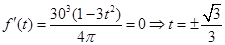
所以函數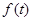 在
在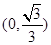 上單調遞增,在
上單調遞增,在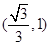 上單調遞減,
上單調遞減,
即當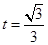 時,體積
時,體積 取得最大值
取得最大值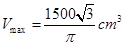 .
.
【解法2】:(1)連接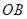 ,在
,在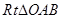 中,設
中,設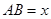 ,則
,則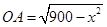
設圓柱底面半徑為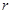 ,則
,則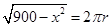 ,即
,即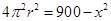 ,
,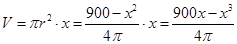 ,其中
,其中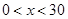 .
.
(2)由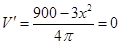 ,得
,得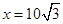 ;
;
由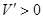 解得
解得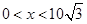 ;由
;由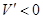 解得
解得 .
.
因此 在
在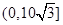 上是增函數,在
上是增函數,在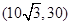 上是減函數.
上是減函數.
所以當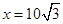 時,
時, 有最大值.
有最大值.
考點:1.導數在最大值、最小值問題中的應用;2.解三角形.


科目:高中數學 來源: 題型:解答題
已知函數f(x)=aln x= (a為常數).
(a為常數).
(1)若曲線y=f(x)在點(1,f(1))處的切線與直線x+2y-5=0垂直,求a的值;
(2)求函數f(x)的單調區間;
(3)當x≥1時,f(x)≤2x-3恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=ex-kx2,x∈R.
(1)若k=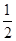 ,求證:當x∈(0,+∞)時,f(x)>1;
,求證:當x∈(0,+∞)時,f(x)>1;
(2)若f(x)在區間(0,+∞)上單調遞增,試求k的取值范圍;
(3)求證: <e4(n∈N*)..
<e4(n∈N*)..
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數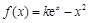 (其中
(其中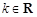 ,e是自然對數的底數).
,e是自然對數的底數).
(Ⅰ)若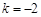 ,試判斷函數
,試判斷函數 在區間
在區間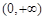 上的單調性;
上的單調性;
(Ⅱ)若函數 有兩個極值點
有兩個極值點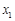 ,
,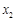 (
(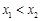 ),求k的取值范圍;
),求k的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,試證明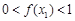 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com