Question

8．已知函數f（x）=|2x-1|+x．
（1）根據絕對值和分段函數知識，將f（x）寫成分段函數；
（2）在如圖的直角坐標系中畫出函數f（x）的圖象，根據圖象，寫出函數的單調區間、值域（不要求證明）；
（3）若在區間[$\frac{1}{2}$，+∞）上，滿足f（a）＞f（3a-2），求實數a的取值范圍．

Answer 1

分析 （1）根據根據絕對值和分段函數知識，將f（x）寫成分段函數即可，
（2）描點畫圖即可，并寫出單調區間，
（3）根據函數的單調性得到，關于a的不等式，解得即可．

解答 解：（1）$f（x）=\left\{{\begin{array}{l}{3x-1}&{x≥\frac{1}{2}}\\{-x+1}&{x＜\frac{1}{2}}\end{array}}\right.$；
（2）單調增區間$[{\frac{1}{2}，+∞}）$，單調減區間$（{-∞，\frac{1}{2}}）$，值域：$[{\frac{1}{2}，+∞}）$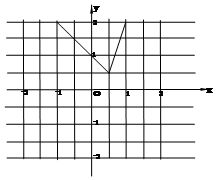

（3）在區間$[{\frac{1}{2}，+∞}）$上，f（x）單調性增，不等式滿足$\left\{\begin{array}{l}{a≥\frac{1}{2}}\\{3a-2≥\frac{1}{2}}\\{a＞3a-2}\end{array}\right.$，
解得：$\frac{5}{6}≤a＜1$．

點評 本題考查了絕對函數和分段函數的圖象和性質和不等式組的解法，屬于基礎題．