Question

已知f（x）為R上不恒為零的函數，且對于任意的a，b∈R都滿足：f=af（b）+bf（a）．
（1）求f（0），f（1）的值；
（2）判斷f（x）的奇偶性，并證明你的結論；
（3）若f（2）=2，g（n）=f（2ⁿ）（n∈N），求g（n）．

Answer 1

【答案】分析：（1）根據題意，用賦值法，令a=b=0，可得f（0）的值，令a=b=1，可得f（1）=f（1）+f（1），即可得f（1）；
（2）由（1）中f（1）=0的結論；再令a=b=-1，則f（1）=-2f（-1）=0，可得f（-1）的值，進而令a=x，b=-1，則f（-x）=-f（x）+xf（-1）=-f（x），即可得答案；
（3）根據題意，f（2ⁿ）=f（2×2^n-1）=2f（2^n-1）+2^n-1f（2），又由f（2）=2，可得f（2ⁿ）=f（2^n-1）+2ⁿ，進而等式可以變形為=2，則數列{f（2ⁿ）}是首項為f（2）=2，公比為2的等比數列，由等比數列的通項公式可得答案．
解答：解：（1）根據題意，對于任意的a，b∈R都滿足：f（a•b）=af（b）+bf（a），
令a=b=0，可得f（0）=0，
令a=b=1，可得f（1）=f（1）+f（1），即f（1）=0；
（2）由（1）的結論，f（1）=0；
令a=b=-1，則f（1）=-2f（-1）=0，∴f（-1）=0
令a=x，b=-1，則f（-x）=-f（x）+xf（-1）=-f（x）
f（x）為奇函數．
（3）根據題意，f（2ⁿ）=f（2×2^n-1）=2f（2^n-1）+2^n-1f（2），
又由f（2）=2，則f（2ⁿ）=f（2^n-1）+2ⁿ，
等式左右兩邊同除2ⁿ可得=，即=2，
則數列{f（2ⁿ）}是首項為f（2）=2，公比為2的等比數列，
則f（2ⁿ）=2ⁿ，
故g（n）=f（2ⁿ）=2ⁿ．
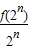
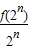點評：本題考查數列與抽象函數的應用，對于抽象函數一般用賦值法，本題的難點在于將f（2ⁿ）=f（2^n-1）+2ⁿ，通過在等式左右兩邊同除2ⁿ，得到=，由等比數列的性質來解題．