解:(1)由題意設橢圓標準方程為

.
由已知得,

.(2分)
則

,∴

.解得a
2=6(4分)
∴所求橢圓方程為

(5分)
(2)令M(x
1,y
1),則

(7分)
∵點M在橢圓上,∴

,故|y
1|的最大值為

(8分)
∴當

時,

的最大值為

.(9分)
(3)假設存在一點P,使
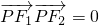
,
∵

,∴

,(10分)
∴△PF
1F
2為直角三角形,∴|PF
1|
2+|PF
2|
2=|F
1F
2|
2=4 ①(11分)
又∵

②(12分)
∴②
2-①,得2|PF
1|•|PF
2|=20,∴

,(13分)
即

=5,由(1)得

最大值為

,故矛盾,
∴不存在一點P,使
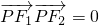
.(14分)
分析:(1)由題意設出橢圓標準方程,根據頂點的坐標和離心率得

,根據a
2=b
2+c
2求出a的值,即求出橢圓標準方程;
(2)根據(1)求出的橢圓標準方程,求出點M縱坐標的范圍,即求出三角形面積的最大值;
(3)先假設存在點P滿足條件,根據向量的數量積得

,根據橢圓的焦距和橢圓的定義列出兩個方程,求出

的值,結合(2)中三角形面積的最大值,判斷出是否存在點P.
點評:本題考查了橢圓方程的求法以及橢圓的性質、向量數量積的幾何意義,利用a、b、c、e幾何意義和a
2=b
2+c
2求出a和b的值,根據橢圓上點的坐標范圍求出相應三角形的面積最值,即根據此范圍判斷點P是否存在,此題綜合性強,涉及的知識多,考查了分析問題和解決問題的能力.

 ),離心率為
),離心率為 ,左、右焦點分別為F1和F2.
,左、右焦點分別為F1和F2.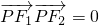 ,若存在,請求出點P的坐標;若不存在,請說明理由.
,若存在,請求出點P的坐標;若不存在,請說明理由. .
. .(2分)
.(2分) ,∴
,∴ .解得a2=6(4分)
.解得a2=6(4分) (5分)
(5分) (7分)
(7分) ,故|y1|的最大值為
,故|y1|的最大值為 (8分)
(8分) 時,
時, 的最大值為
的最大值為 .(9分)
.(9分)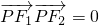 ,
, ,∴
,∴ ,(10分)
,(10分) ②(12分)
②(12分) ,(13分)
,(13分) =5,由(1)得
=5,由(1)得 最大值為
最大值為 ,故矛盾,
,故矛盾,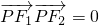 .(14分)
.(14分) ,根據a2=b2+c2求出a的值,即求出橢圓標準方程;
,根據a2=b2+c2求出a的值,即求出橢圓標準方程; ,根據橢圓的焦距和橢圓的定義列出兩個方程,求出
,根據橢圓的焦距和橢圓的定義列出兩個方程,求出 的值,結合(2)中三角形面積的最大值,判斷出是否存在點P.
的值,結合(2)中三角形面積的最大值,判斷出是否存在點P.

 ),離心率為
),離心率為 ,左、右焦點分別為F1和F2.
,左、右焦點分別為F1和F2. ,若存在,請求出點P的坐標;若不存在,請說明理由.
,若存在,請求出點P的坐標;若不存在,請說明理由.