
【題目】鯉魚是中國五千年文化傳承的載體之一,它既是拼搏進取、敢于突破自我、敢于冒險奮進精神的載體,又是富裕、吉慶、幸運的美好象征.某水產養殖研究所為發揚傳統文化,準備進行“中國紅鯉”和“中華彩鯉”雜交育種實驗.研究所對200尾中國紅鯉和160尾中華彩鯉幼苗進行2個月培育后,將根據體長分別選擇生長快的10尾中國紅鯉和8尾中華彩鯉作為種魚進一步培育.為了解培育2個月后全體幼魚的體長情況,按照品種進行分層抽樣,其中共抽取40尾中國紅鯉的體長數據(單位:![]() )如下:
)如下:
5 | 6 | 7 | 7.5 | 8 | 8.4 | 4 | 3.5 | 4.5 | 4.3 |
5 | 4 | 3 | 2.5 | 4 | 1.6 | 6 | 6.5 | 5.5 | 5.7 |
3.1 | 5.2 | 4.4 | 5 | 6.4 | 3.5 | 7 | 4 | 3 | 3.4 |
6.9 | 4.8 | 5.6 | 5 | 5.6 | 6.5 | 3 | 6 | 7 | 6.6 |
(1)根據以上樣本數據推斷,若某尾中國紅鯉的體長為![]() ,它能否被選為種魚?說明理由;
,它能否被選為種魚?說明理由;
(2)通過計算得到中國紅鯉樣本數據平均值為![]() ,中華彩鯉樣本數據平均值為
,中華彩鯉樣本數據平均值為![]() ,求所有樣本數據的平均值;
,求所有樣本數據的平均值;
(3)如果將8尾中華彩鯉種魚隨機兩兩組合,求體長最長的2尾組合到一起的概率.
【答案】(1)能;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據樣本數據中能被選為種魚的身長數據,可知![]() 能被選為種魚;(2)根據分層抽樣原則得到中華彩鯉的樣本數,根據平均數計算方法求解得到結果;(3)列出與體長最長的
能被選為種魚;(2)根據分層抽樣原則得到中華彩鯉的樣本數,根據平均數計算方法求解得到結果;(3)列出與體長最長的![]() 尾中的
尾中的![]() 尾組合到一起的所有情況,根據古典概型求得結果.
尾組合到一起的所有情況,根據古典概型求得結果.
(1)能被選為種魚
![]() 尾中國紅鯉中有
尾中國紅鯉中有![]() 尾能被選為種魚
尾能被選為種魚 ![]() 尾中國紅鯉樣本中有
尾中國紅鯉樣本中有![]() 尾能被選為種魚
尾能被選為種魚
樣本數據中身長為![]() 和
和![]() 的中國紅鯉能被選為種魚
的中國紅鯉能被選為種魚
身長為![]() 以下的中國紅鯉不能被選為種魚
以下的中國紅鯉不能被選為種魚
由于![]() ,所以該尾中國紅鯉能被選為種魚
,所以該尾中國紅鯉能被選為種魚
(2)根據分層抽樣的原則,抽取中華彩鯉樣本數為![]() 尾
尾
![]() 所有樣本數據平均值為
所有樣本數據平均值為![]()
![]()
(3)記體長最長的![]() 尾中華彩鯉為
尾中華彩鯉為![]() ,其他
,其他![]() 尾中華彩鯉為
尾中華彩鯉為![]()
與![]() 組合的中華彩鯉,共有
組合的中華彩鯉,共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七種情況
七種情況
所以,體長最長的![]() 尾組合到一起的的概率為
尾組合到一起的的概率為![]()


科目:高中數學 來源: 題型:
【題目】下圖是古希臘數學家阿基米德用平衡法求球的體積所用的圖形.此圖由正方形![]() 、半徑為
、半徑為![]() 的圓及等腰直角三角形構成,其中圓內切于正方形,等腰三角形的直角頂點與
的圓及等腰直角三角形構成,其中圓內切于正方形,等腰三角形的直角頂點與![]() 的中點
的中點![]() 重合,斜邊在直線
重合,斜邊在直線![]() 上.已知
上.已知![]() 為
為![]() 的中點,現將該圖形繞直線
的中點,現將該圖形繞直線![]() 旋轉一周,則陰影部分旋轉后形成的幾何體積為( )
旋轉一周,則陰影部分旋轉后形成的幾何體積為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次測驗中,某班40名考生的成績滿分100分統計如圖所示.

(Ⅰ)估計這40名學生的測驗成績的中位數![]() 精確到0.1;
精確到0.1;
(Ⅱ)記80分以上為優秀,80分及以下為合格,結合頻率分布直方圖完成下表,并判斷是否有95%的把握認為數學測驗成績與性別有關?
合格 | 優秀 | 合計 | |
男生 | 16 | ||
女生 | 4 | ||
合計 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“愛國,是人世間最深層、最持久的情感,是一個人立德之源、立功之本。”在中華民族幾千年綿延發展的歷史長河中,愛國主義始終是激昂的主旋律。愛國汽車公司擬對“東方紅”款高端汽車發動機進行科技改造,根據市場調研與模擬,得到科技改造投入![]() (億元)與科技改造直接收益
(億元)與科技改造直接收益![]() (億元)的數據統計如下:
(億元)的數據統計如下:
| 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
| 13 | 22 | 31 | 42 | 50 | 56 | 58 | 68.5 | 68 | 67.5 | 66 | 66 |
當![]() 時,建立了
時,建立了![]() 與
與![]() 的兩個回歸模型:模型①:
的兩個回歸模型:模型①:![]() ;模型②:
;模型②:![]() ;當
;當![]() 時,確定
時,確定![]() 與
與![]() 滿足的線性回歸方程為:
滿足的線性回歸方程為:![]() .
.
(1)根據下列表格中的數據,比較當![]() 時模型①、②的相關指數
時模型①、②的相關指數![]() ,并選擇擬合精度更高、更可靠的模型,預測對“東方紅”款汽車發動機科技改造的投入為17億元時的直接收益.
,并選擇擬合精度更高、更可靠的模型,預測對“東方紅”款汽車發動機科技改造的投入為17億元時的直接收益.
回歸模型 | 模型① | 模型② |
回歸方程 |
|
|
| 182.4 | 79.2 |
(附:刻畫回歸效果的相關指數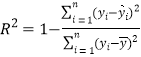 ,
,![]() .)
.)
(2)為鼓勵科技創新,當科技改造的投入不少于20億元時,國家給予公司補貼收益10億元,以回歸方程為預測依據,比較科技改造投入17億元與20億元時公司實際收益的大小;
(附:用最小二乘法求線性回歸方程![]() 的系數公式
的系數公式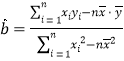
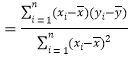 ;
;![]() )
)
(3)科技改造后,“東方紅”款汽車發動機的熱效![]() 大幅提高,
大幅提高,![]() 服從正態分布
服從正態分布![]() ,公司對科技改造團隊的獎勵方案如下:若發動機的熱效率不超過
,公司對科技改造團隊的獎勵方案如下:若發動機的熱效率不超過![]() ,不予獎勵;若發動機的熱效率超過
,不予獎勵;若發動機的熱效率超過![]() 但不超過
但不超過![]() ,每臺發動機獎勵2萬元;若發動機的熱效率超過
,每臺發動機獎勵2萬元;若發動機的熱效率超過![]() ,每臺發動機獎勵5萬元.求每臺發動機獲得獎勵的數學期望.
,每臺發動機獎勵5萬元.求每臺發動機獲得獎勵的數學期望.
(附:隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
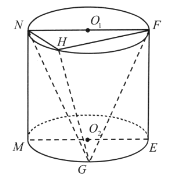
【題目】如圖,在圓柱![]() 中,點
中,點![]() 、
、![]() 分別為上、下底面的圓心,平面
分別為上、下底面的圓心,平面![]() 是軸截面,點
是軸截面,點![]() 在上底面圓周上(異于
在上底面圓周上(異于![]() 、
、![]() ),點
),點![]() 為下底面圓弧
為下底面圓弧![]() 的中點,點
的中點,點![]() 與點
與點![]() 在平面
在平面![]() 的同側,圓柱
的同側,圓柱![]() 的底面半徑為1,高為2.
的底面半徑為1,高為2.
(1)若平面![]() 平面
平面![]() ,證明:
,證明:![]() ;
;
(2)若直線![]() 平面
平面![]() ,求
,求![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列結論正確的是( ).
A.“![]() ,
,![]() 互為共軛復數”是“
互為共軛復數”是“![]() ”的充分不必要條件
”的充分不必要條件
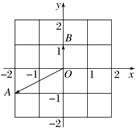
B.如圖,在復平面內,若復數![]() ,
,![]() 對應的向量分別是
對應的向量分別是![]() ,
,![]() ,則復數
,則復數![]() 對應的點的坐標為
對應的點的坐標為![]()
C.若函數![]() 恰在
恰在![]() 上單調遞減,則實數
上單調遞減,則實數![]() 的值為4
的值為4
D.函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為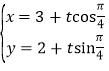 (其中
(其中![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,并取相同的單位長度,曲線
軸正半軸為極軸建立極坐標系,并取相同的單位長度,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)過點![]() 作直線
作直線![]() 的垂線交曲線
的垂線交曲線![]() 于
于![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
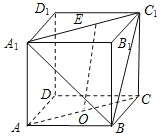
【題目】在正方體ABCD﹣A1B1C1D1中,O為線段AC的中點,點E在線段A1C1上,則直線OE與平面A1BC1所成角的正弦值的取值范圍是( )
A.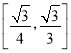 B.
B.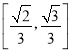 C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com