
設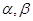 都是銳角,且
都是銳角,且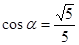 ,
,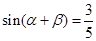 ,則
,則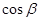 =( )
=( )
A.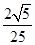 B.
B.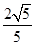 C.
C.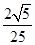 或
或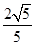 D.
D.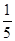 或
或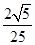
B
【解析】
試題分析:由α、β都是銳角,且cosα值小于 ,得到sinα大于0,利用余弦函數的圖象與性質得出α的范圍,再由sin(α+β)的值大于
,得到sinα大于0,利用余弦函數的圖象與性質得出α的范圍,再由sin(α+β)的值大于 ,利用正弦函數的圖象與性質得出α+β為鈍角,可得出cos(α+β)小于0,然后利用同角三角函數間的基本關系分別求出sinα和cos(α+β)的值,將所求式子中的角β變形為(α+β)-α,利用兩角和與差的余弦函數公式化簡后,把各自的值代入即可求出值.解:∵α、β都是銳角,且cosα=
,利用正弦函數的圖象與性質得出α+β為鈍角,可得出cos(α+β)小于0,然后利用同角三角函數間的基本關系分別求出sinα和cos(α+β)的值,將所求式子中的角β變形為(α+β)-α,利用兩角和與差的余弦函數公式化簡后,把各自的值代入即可求出值.解:∵α、β都是銳角,且cosα=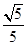
< ,∴
,∴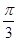 <α<
<α<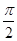 ,又sin(α+β)=
,又sin(α+β)=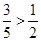 ∴
∴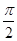 <α+β<π,∴cos(α+β)=-
<α+β<π,∴cos(α+β)=-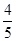 ,sinα=
,sinα=
則cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=- 故選B
故選B
考點:同角三角函數間的基本關系
點評:此題考查了同角三角函數間的基本關系,正弦、余弦函數的圖象與性質,以及兩角和與差的余弦函數公式,熟練掌握公式及基本關系是解本題的關鍵.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com