【題目】某幼兒園雛鷹班的生活老師統計2018年上半年每個月的20日的晝夜溫差
，
和患感冒的小朋友人數（
/人）的數據如下：
溫差 |
|
|
|
|
|
|
患感冒人數 | 8 | 11 | 14 | 20 | 23 | 26 |
其中
，
，
.
（Ⅰ）請用相關系數加以說明是否可用線性回歸模型擬合與
（Ⅱ）建立關于
的回歸方程（精確到
），預測當晝夜溫差升高
時患感冒的小朋友的人數會有什么變化？（人數精確到整數）
參考數據：
．參考公式：相關系數：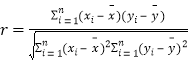
，回歸直線方程是
，
,
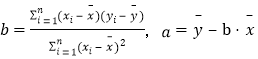科目：高中數學 來源： 題型：
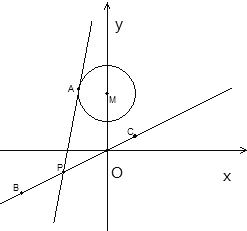
【題目】已知圓M：
，設點B，C是直線l：
上的兩點，它們的橫坐標分別是t，
，P點的縱坐標為a且點P在線段BC上，過P點作圓M的切線PA，切點為A
若
，
，求直線PA的方程；
經過A，P，M三點的圓的圓心是D，
將
表示成a的函數
，并寫出定義域．
求線段DO長的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C的兩個焦點分別為F1（-1，0）、F2（1，0），短軸的兩個端點分別為B1，B2
（1）若△F1B1B2為等邊三角形，求橢圓C的方程；
（2）若橢圓C的短軸長為2，過點F2的直線l與橢圓C相交于P，Q兩點，且
，求直線l的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
(a>b>0)的離心率為
，短軸長為2.直線l：y＝kx＋m與橢圓C交于M，N兩點，又l與直線
， 
分別交于A，B兩點，其中點A在第一象限，點B在第二象限，且△OAB的面積為2(O為坐標原點).
(1)求橢圓C的方程；
(2)求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在發生公共衛生事件期間，有專業機構認為該事件在一段時間內沒有發生大規模群體感染的標志為“連續
天，每天新增疑似病例不超過
人”．過去日，甲、乙、丙、丁四地新增疑似病例數據信息如下，則一定符合該標志的是（ ）
甲地：總體平均數
，且中位數為
；
乙地：總體平均數為
，且標準差
；
丙地：總體平均數，且極差
；
丁地：眾數為
，且極差
．
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解某班學生喜愛打籃球是否與性別有關，對本班50人進行了問卷調查得到了如下的列聯表：
喜愛打籃球 | 不喜愛打籃球 | 合計 | |
男生 | 5 | ||
女生 | 10 | ||
合計 | 50 |
已知在全部50人中隨機抽取1人抽到喜愛打籃球的學生的概率為
．
（1）請將上面的列聯表補充完整；
（2）是否有99%的把握認為“喜愛打籃球與性別有關”？說明你的理由．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著人口老齡化的到來，我國的勞動力人口在不斷減少，“延遲退休”已經成為人們越來越關注的話題，為了解公眾對“延遲退休”的態度，某校課外研究性學習小組在某社區隨機抽取了50人進行調查，將調查情況進行整理后制成下表：
年齡 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人數 | 4 | 5 | 8 | 5 | 3 |
年齡 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人數 | 6 | 7 | 3 | 5 | 4 |
經調查年齡在［25,30),[55,60）的被調查者中贊成“延遲退休”的人數分別是3人和2人.現從這兩組的被調查者中各隨機選取2人，進行跟蹤調查．
（I）求年齡在［25,30）的被調查者中選取的2人都贊成“延遲退休”的概率；
（II）若選中的4人中，不贊成“延遲退休”的人數為
，求隨機變量
的分布列和數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
