Question

函數y=f(x)是定義在R上的偶函數，當x∈[-1，0]時，f(x)=-tx³+tx，記函數f(x)的圖象在x=處的切線為l，f′()=1．

    (Ⅰ)當x∈[0，1]時，求函數f(x)的解析式；

    (Ⅱ)求切線l的方程；

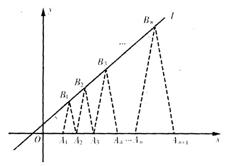
    (Ⅲ)點列B₁(b₁，2)，B₂(b₂，3)，…，B_n(b_n，n+1)在l上，A₁(x₁，0)，A₂(x₂，0)，…，A_n(x_n，0)依次為x軸上的點，如圖，當n∈N*，點A_n、B_n、A_n+1構成以A_nA_n+1為底邊的等腰三角形．若x₁=a(0＜a＜1)，且數列{x_n}是等差數列，求a的值和數列{x_n}的通項公式．

Answer 1

答案：解：(Ⅰ)當0≤x≤1時，則-1≤-x≤0，

∴f(-x)=-t(-x)³+t·(-x)．

∵f(-x)=f(x)，

∴f(x)=tx³-tx，x∈[0，1]．

∴f′(x)=3tx²-t，由于f′()=1，∴t=-4．

∴f(x)=-4x³+4x(x∈[0，1])． 

(Ⅱ)由題意切點為(，f())即(，)，l的斜率為k₁=f′()=1，

由直線點斜式方程知l的方程為y=x+1．

(Ⅲ)∵點B_n(b_n，n+1)在直線y=x+1上，

∴b_n=n．

∴=n，即x_n+x_n+1=2n．

由此有：x_n+1+x_n+2=2n+2．

兩式相減得：x_n+2-x_n=2．

∴數列{x_n}的所有奇數項、所有偶數項分別構成以2為公差的等差數列．

又x₁+x₂=2，x₁=a，∴x₂=2-a．

∴x_2n-1=x₁+2(n-1)=(2n-1)+a-1，

x_2n=x₂+2(n-1)=2-a+2n-2=2n-a．

當且僅當a-1=-a即a=時，{x_n}為等差數列．

此時數列{x_n}的通項公式為x_n=n-． 

(Ⅲ)另解：同前得x_n+1+x_n=2n，即x_n+1=-x_n+2n．

記x_n+1+p(n+1)+q=-(x_n+pn+q)，

展開得：x_n+1=-x_n-2pn-2q-p，

比較得，解得p=-1，q=．

∴x_n+1-(n+1)+=-(x_n-n+)．

令b_n=x_n-n+，則上式為b_n+1=-b_n，

∴{b_n}是以-1為公比，首項為b₁=x₁-1+=a-的等比數列.

∴b_n=(a-)(-1)ⁿ，

即x_n-n+=(a-)(-1)ⁿ．

∴x_n=(a-)(-1)ⁿ+n-．

∵{x_n}是等差數列，

∴a-=0，即a=．

此時，x_n=n-．