【題目】如圖，圓形紙片的圓心為O，半徑為5 cm，該紙片上的等邊三角形ABC的中心為O。D、E、F為圓O上的點，△DBC，△ECA，△FAB分別是以BC，CA，AB為底邊的等腰三角形。沿虛線剪開后，分別以BC，CA，AB為折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱錐。當△ABC的邊長變化時，所得三棱錐體積（單位：cm3）的最大值為_______。
黃岡小狀元滿分沖刺微測驗系列答案
新輔教導學系列答案
陽光同學一線名師全優好卷系列答案科目：高中數學 來源： 題型：
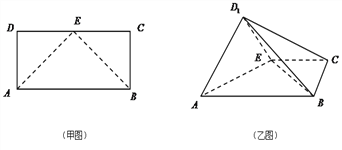
【題目】【2017四川宜賓二診】如甲圖所示，在矩形
中， 
， 
， 
是
的中點，將
沿
折起到
位置，使平面
平面
，得到乙圖所示的四棱錐
．
（Ⅰ）求證： 
平面
；
（Ⅱ）求二面角
的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知A（x1 ， y1），B（x2 ， y2）是函數f（x）=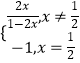 
的圖象上的任意兩點（可以重合），點M在直線x= 
上，且 
= 
．
（1）求x1+x2的值及y1+y2的值；
（2）已知S1=0，當n≥2時，Sn=f（ 
）+f（ 
）+f（ 
）+…+f（ 
），求Sn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】把函數f（x）=sin（2x+φ）（|φ|＜ 
）的圖象上的所有點向左平移 
個單位長度，得到函數y=g（x）的圖象，且g（﹣x）=g（x），則（ ）
A.y=g（x）在（0， ）單調遞增，其圖象關于直線x= 
對稱
B.y=g（x）在（0， ）單調遞增，其圖象關于直線x= 對稱
C.y=g（x）在（0， ）單調遞減，其圖象關于直線x= 對稱
D.y=g（x）在（0， ）單調遞減，其圖象關于直線x= 對稱
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（4，3）， 
=（2，﹣1），O為坐標原點，P是直線AB上一點．
（1）若點P是線段AB的中點，求向量 與向量 夾角θ的余弦值；
（2）若點P在線段AB的延長線上，且| 
|= 
| 
|，求點P的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知在四棱錐P﹣ABCD中，底面ABCD是平行四邊形，PA⊥平面ABCD，PA= 
，AB=1．AD=2．∠BAD=120°，E，F，G，H分別是BC，PB，PC，AD的中點．
（Ⅰ）求證：PH∥平面GED；
（Ⅱ）過點F作平面α，使ED∥平面α，當平面α⊥平面EDG時，設PA與平面α交于點Q，求PQ的長．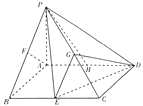
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比，收獲時各隨機抽取了100個網箱，測量各箱水產品的產量（單位：kg）, 其頻率分布直方圖如下：
（1）記A表示事件“舊養殖法的箱產量低于50 kg”，估計A的概率；
（2）填寫下面列聯表，并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關：
箱產量＜50 kg | 箱產量≥50 kg | |
舊養殖法 | ||
新養殖法 |
（3）根據箱產量的頻率分布直方圖，對這兩種養殖方法的優劣進行比較.
附：
P（ | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
