
【題目】已知等差數列{an}和等比數列{bn},其中{an}的公差不為0.設Sn是數列{an}的前n項和.若a1 , a2 , a5是數列{bn}的前3項,且S4=16.
(1)求數列{an}和{bn}的通項公式;
(2)若數列{ ![]() }為等差數列,求實數t;
}為等差數列,求實數t;
(3)構造數列a1 , b1 , a2 , b1 , b2 , a3 , b1 , b2 , b3 , …,ak , b1 , b2 , …,bk , …,若該數列前n項和Tn=1821,求n的值.
【答案】
(1)解:設{an}的公差d≠0.∵a1,a2,a5是數列{bn}的前3項,且S4=16.
∴ ![]() ,即
,即 ![]() ,4a1+
,4a1+ ![]() =16,
=16,
解得a1=1,d=2,
∴an=1+(n﹣1)×2=2n﹣1.
∴b1=1,b2=3,公比q=3.
∴bn=3n﹣1
(2)解:Sn= ![]() =n2.∴
=n2.∴ ![]() =
= ![]() .
.
∵數列{ ![]() }為等差數列,
}為等差數列,
∴ ![]() =
= ![]() +
+ ![]() ,t2﹣2t=0.
,t2﹣2t=0.
解得t=2或0,經過驗證滿足題意
(3)解:由(1)可得:Sn=n2,數列{bn}的前n項和An= ![]() =
= ![]() .數列{An}的前n項和Un=
.數列{An}的前n項和Un= ![]() ﹣
﹣ ![]() n=
n= ![]() ﹣
﹣ ![]() n.
n.
數列a1,b1,a2,b1,b2,a3,b1,b2,b3,…,ak,b1,b2,…,bk,…,
∴該數列前k+ ![]() =
= ![]() 項和=k2+
項和=k2+ ![]() ﹣
﹣ ![]() (k﹣1),
(k﹣1),
∵37=2187,38=6561.
∴取k=8,可得前 ![]() =36項的和為:
=36項的和為: ![]() =1700,
=1700,
令Tn=1821=1700+ ![]() ,解得m=5.
,解得m=5.
∴n=36+5=41
【解析】(1)設{an}的公差d≠0.由a1 , a2 , a5是數列{bn}的前3項,且S4=16.可得 ![]() ,即
,即 ![]() ,4a1+
,4a1+ ![]() =16,解得a1 , d,即可得出.(2)Sn=
=16,解得a1 , d,即可得出.(2)Sn= ![]() =n2 . 可得
=n2 . 可得 ![]() =
= ![]() .根據數列{
.根據數列{ ![]() }為等差數列,可得
}為等差數列,可得 ![]() =
= ![]() +
+ ![]() ,t2﹣2t=0. 解得t.(3)由(1)可得:Sn=n2 , 數列{bn}的前n項和An=
,t2﹣2t=0. 解得t.(3)由(1)可得:Sn=n2 , 數列{bn}的前n項和An= ![]() =
= ![]() .數列{An}的前n項和Un=
.數列{An}的前n項和Un= ![]() ﹣
﹣ ![]() n=
n= ![]() ﹣
﹣ ![]() n.數列a1 , b1 , a2 , b1 , b2 , a3 , b1 , b2 , b3 , …,ak , b1 , b2 , …,bk , …,可得:該數列前k+
n.數列a1 , b1 , a2 , b1 , b2 , a3 , b1 , b2 , b3 , …,ak , b1 , b2 , …,bk , …,可得:該數列前k+ ![]() =
= ![]() 項和=k2+
項和=k2+ ![]() ﹣
﹣ ![]() (k﹣1),根據37=2187,38=6561.進而得出.
(k﹣1),根據37=2187,38=6561.進而得出.


科目:高中數學 來源: 題型:
【題目】已知如圖:平行四邊形ABCD中,BC=6,正方形ADEF所在平面與平面ABCD垂直,G,H分別是DF,BE的中點. 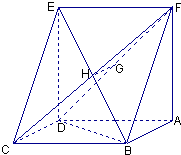
(1)求證:GH∥平面CDE;
(2)若CD=2,DB=4 ![]() ,求四棱錐F﹣ABCD的體積.
,求四棱錐F﹣ABCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=aln x+![]() (a>0).
(a>0).
(1)求函數f(x)的極值;
(2)若對任意的x>0,恒有ax(2-ln x)≤1,求實數a的取值范圍;
(3)是否存在實數a,使得函數f(x)在[1,e]上的最小值為0?若存在,試求出a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三角形的頂點分別為A(﹣1,3),B(3,2),C(1,0)
(1)求BC邊上高的長度;
(2)若直線l過點C,且在l上不存在到A,B兩點的距離相等的點,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了解學校食堂的服務情況,隨機調查了50名就餐的教師和學生.根據這50名師生對餐廳服務質量進行評分,繪制出了頻率分布直方圖(如圖所示),其中樣本數據分組為[40,50),[50,60),…,[90,100]. 
(1)求頻率分布直方圖中a的值;
(2)從評分在[40,60)的師生中,隨機抽取2人,求此人中恰好有1人評分在[40,50)上的概率;
(3)學校規定:師生對食堂服務質量的評分不得低于75分,否則將進行內部整頓,試用組中數據估計該校師生對食堂服務質量評分的平均分,并據此回答食堂是否需要進行內部整頓.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市的教育主管部門對所管轄的學校進行年終督導評估,為了解某學校師生對學校教學管理的滿意度,分別從教師和不同年級的同學中隨機抽取若干師生,進行評分(滿分100分),繪制如下頻率分布直方圖(分組區間為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ),并將分數從低到高分為四個等級:
),并將分數從低到高分為四個等級:
滿意度評分 |
|
|
|
|
滿意度等級 | 不滿意 | 基本滿意 | 滿意 | 非常滿意 |
已知滿意度等級為基本滿意的有340人.

(1)求表中![]() 的值及不滿意的人數;
的值及不滿意的人數;
(2)在等級為不滿意的師生中,老師占![]() ,現從該等級師生中按分層抽樣抽取12人了解不滿意的原因,并從中抽取3人擔任整改督導員,記
,現從該等級師生中按分層抽樣抽取12人了解不滿意的原因,并從中抽取3人擔任整改督導員,記![]() 為老師整改督導員的人數,求
為老師整改督導員的人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com