
【題目】已知橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
, ![]() ,且離心率為
,且離心率為![]() ,
, ![]() 為橢圓上任意一點,當(dāng)
為橢圓上任意一點,當(dāng)![]() 時,
時, ![]() 的面積為1.
的面積為1.
(1)求橢圓![]() 的方程;
的方程;
(2)已知點![]() 是橢圓
是橢圓![]() 上異于橢圓頂點的一點,延長直線
上異于橢圓頂點的一點,延長直線![]() ,
, ![]() 分別與橢圓交于點
分別與橢圓交于點![]() ,
, ![]() ,設(shè)直線
,設(shè)直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求證:
,求證: ![]() 為定值.
為定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)設(shè)![]() 由題
由題 ,由此求出
,由此求出![]() ,可得橢圓
,可得橢圓![]() 的方程;
的方程;
(2)設(shè)![]() ,
, ![]() ,
,
當(dāng)直線![]() 的斜率不存在時,可得
的斜率不存在時,可得![]() ;
;
當(dāng)直線![]() 的斜率不存在時,同理可得
的斜率不存在時,同理可得![]() .
.
當(dāng)直線![]() 、
、![]() 的斜率存在時,
的斜率存在時,![]() ,
,
設(shè)直線![]() 的方程為
的方程為![]() ,則由
,則由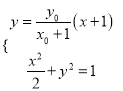 消去
消去![]() 通過運算可得
通過運算可得
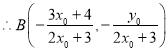 ,同理可得
,同理可得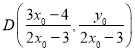 ,由此得到直線
,由此得到直線![]() 的斜率為
的斜率為![]() ,
,
![]() 直線
直線![]() 的斜率為
的斜率為![]() ,進而可得
,進而可得![]() .
.
試題解析:(1)設(shè)![]() 由題
由題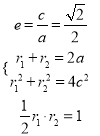 ,
,
解得![]() ,則
,則![]() ,
,
![]() 橢圓
橢圓![]() 的方程為
的方程為![]() .
.
(2)設(shè)![]() ,
, ![]() ,
,
當(dāng)直線![]() 的斜率不存在時,設(shè)
的斜率不存在時,設(shè)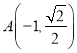 ,則
,則 ,
,
直線![]() 的方程為
的方程為![]() 代入
代入![]() ,可得
,可得![]() ,
,
![]() ,
, ![]() ,則
,則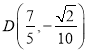 ,
,
![]() 直線
直線![]() 的斜率為
的斜率為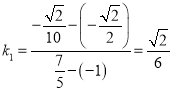 ,直線
,直線![]() 的斜率為
的斜率為![]() ,
,
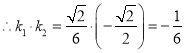 ,
,
當(dāng)直線![]() 的斜率不存在時,同理可得
的斜率不存在時,同理可得![]() .
.
當(dāng)直線![]() 、
、![]() 的斜率存在時,
的斜率存在時,![]() ,
,
設(shè)直線![]() 的方程為
的方程為![]() ,則由
,則由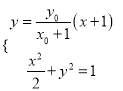 消去
消去![]() 可得:
可得:
![]() ,
,
又![]() ,則
,則![]() ,代入上述方程可得
,代入上述方程可得
![]() ,
,
![]() ,則
,則![]()
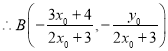 ,
,
設(shè)直線![]() 的方程為
的方程為![]() ,同理可得
,同理可得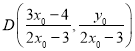 ,
,
![]() 直線
直線![]() 的斜率為
的斜率為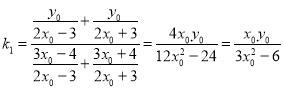 ,
,
![]() 直線
直線![]() 的斜率為
的斜率為![]() ,
,
![]()
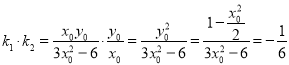 .
.
所以,直線![]() 與
與![]() 的斜率之積為定值
的斜率之積為定值![]() ,即
,即![]() .
.
【題型】解答題
【結(jié)束】
21
【題目】已知函數(shù)![]() ,
, ![]() ,在
,在![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若方程![]() 有兩個實數(shù)根
有兩個實數(shù)根![]() ,
, ![]() ,且
,且![]() ,證明:
,證明: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)見解析
;(2)見解析
【解析】試題分析: ![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求導(dǎo)算出切線方程即可求出結(jié)果
,求導(dǎo)算出切線方程即可求出結(jié)果![]() 構(gòu)造
構(gòu)造![]() ,求導(dǎo),得
,求導(dǎo),得![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,在區(qū)間
上單調(diào)遞減,在區(qū)間![]() 上單調(diào)遞增,設(shè)
上單調(diào)遞增,設(shè)![]() 的根為
的根為![]() ,證得
,證得![]() ,討論證得
,討論證得![]() 的根為
的根為![]() ,
, ![]() ,從而得證結(jié)論
,從而得證結(jié)論
解析:(1)由題意![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,則
,則![]() ,與
,與![]() 矛盾,故
矛盾,故![]() ,
, ![]() .
.
(2)由(Ⅰ)可知![]() ,
, ![]() ,
,
設(shè)![]() 在(-1,0)處的切線方程為
在(-1,0)處的切線方程為![]() ,
,
易得, ![]() ,令
,令![]()
即![]() ,
, ![]() ,
,
當(dāng)![]() 時,
時, ![]()
當(dāng)![]() 時,
時,
設(shè)![]() ,
, ![]() ,
,
故函數(shù)![]() 在
在![]() 上單調(diào)遞增,又
上單調(diào)遞增,又![]() ,
,
所以當(dāng)![]() 時,
時, ![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() ,
,
所以函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,在區(qū)間
上單調(diào)遞減,在區(qū)間![]() 上單調(diào)遞增,
上單調(diào)遞增,
故![]() ,
, ![]() ,
,
設(shè)![]() 的根為
的根為![]() ,則
,則![]() ,
,
又函數(shù)![]() 單調(diào)遞減,故
單調(diào)遞減,故![]() ,故
,故![]() ,
,
設(shè)![]() 在(0,0)處的切線方程為
在(0,0)處的切線方程為![]() ,易得
,易得![]() ,
,
令![]() ,
, ![]() ,
,
當(dāng)![]() 時,
時, ![]() ,
,
當(dāng)![]() 時,
時,
![]()
故函數(shù)![]() 在
在![]() 上單調(diào)遞增,又
上單調(diào)遞增,又![]() ,
,
所以當(dāng)![]() 時,
時, ![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() ,
,
所以函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,在區(qū)間
上單調(diào)遞減,在區(qū)間![]() 上單調(diào)遞增,
上單調(diào)遞增,
![]() ,
, ![]() ,
,
設(shè)![]() 的根為
的根為![]() ,則
,則![]() ,
,
又函數(shù)![]() 單調(diào)遞增,故
單調(diào)遞增,故![]() ,故
,故![]() ,
,
又![]() ,
,
![]() .
.


 同步練習(xí)河南大學(xué)出版社系列答案
同步練習(xí)河南大學(xué)出版社系列答案 同步練習(xí)西南師范大學(xué)出版社系列答案
同步練習(xí)西南師范大學(xué)出版社系列答案 補充習(xí)題江蘇系列答案
補充習(xí)題江蘇系列答案 學(xué)練快車道口算心算速算天天練系列答案
學(xué)練快車道口算心算速算天天練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(n)是定義在N*上的增函數(shù),f(4)=5,且滿足:
①任意n∈N*,f(n)![]() Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表達式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(Ⅰ)設(shè)命題![]() 實數(shù)
實數(shù)![]() 滿足
滿足![]() ,其中
,其中![]() ,命題
,命題![]() 實數(shù)
實數(shù)![]() 滿足
滿足![]() .若
.若![]() 是
是![]() 的充分不必要條件,求實數(shù)
的充分不必要條件,求實數(shù)![]() 的取值范圍.
的取值范圍.
(Ⅱ)已知命題![]() 方程
方程![]() 表示焦點在x軸上雙曲線;命題
表示焦點在x軸上雙曲線;命題![]() 空間向量
空間向量![]() ,
,![]() 的夾角為銳角,如果命題“
的夾角為銳角,如果命題“![]() ”為真,命題“
”為真,命題“![]() ”為假.求
”為假.求![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是公差不為零的等差數(shù)列,滿足
是公差不為零的等差數(shù)列,滿足![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比數(shù)列.
成等比數(shù)列.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)設(shè)數(shù)列![]() 滿足
滿足![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)設(shè)等差數(shù)列![]() 的公差為
的公差為![]() ,由a3=7,且
,由a3=7,且![]() 、
、![]() 、
、![]() 成等比數(shù)列.可得
成等比數(shù)列.可得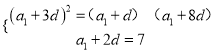 ,解之得即可得出數(shù)列
,解之得即可得出數(shù)列![]() 的通項公式;
的通項公式;
2)由(1)得![]() ,則
,則![]() ,由裂項相消法可求數(shù)列
,由裂項相消法可求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
試題解析:(1)設(shè)數(shù)列![]() 的公差為
的公差為![]() ,且
,且![]() 由題意得
由題意得![]() ,
,
即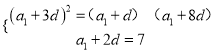 ,解得
,解得![]() ,
,
所以數(shù)列![]() 的通項公式
的通項公式![]() .
.
(2)由(1)得![]()
![]() ,
,
![]()
![]() .
.
【題型】解答題
【結(jié)束】
18
【題目】四棱錐![]() 的底面
的底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 為正三角形.
為正三角形.
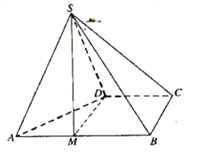
(1)點![]() 為棱
為棱![]() 上一點,若
上一點,若![]() 平面
平面![]() ,
,![]() ,求實數(shù)
,求實數(shù)![]() 的值;
的值;
(2)求點B到平面SAD的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() ,
, ![]() 為參數(shù)),以坐標(biāo)原點
為參數(shù)),以坐標(biāo)原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標(biāo)系,直線
軸正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相切;
相切;
(1)求曲線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)在曲線![]() 上取兩點
上取兩點![]() ,
, ![]() 與原點
與原點![]() 構(gòu)成
構(gòu)成![]() ,且滿足
,且滿足![]() ,求面積
,求面積![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)利用極坐標(biāo)與直角坐標(biāo)的互化公式可得直線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() ,
,
,消去參數(shù)![]() 可知曲線
可知曲線![]() 是圓心為
是圓心為![]() ,半徑為
,半徑為![]() 的圓,由直線
的圓,由直線![]() 與曲線
與曲線![]() 相切,可得:
相切,可得: ![]() ;則曲線C的方程為
;則曲線C的方程為![]() , 再次利用極坐標(biāo)與直角坐標(biāo)的互化公式可得
, 再次利用極坐標(biāo)與直角坐標(biāo)的互化公式可得
可得曲線C的極坐標(biāo)方程.
(2)由(1)不妨設(shè)M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,
![]() ,
,
由此可求![]() 面積的最大值.
面積的最大值.
試題解析:(1)由題意可知直線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() ,
,
曲線![]() 是圓心為
是圓心為![]() ,半徑為
,半徑為![]() 的圓,直線
的圓,直線![]() 與曲線
與曲線![]() 相切,可得:
相切,可得:  ;可知曲線C的方程為
;可知曲線C的方程為![]() ,
,
所以曲線C的極坐標(biāo)方程為![]() ,
,
即![]() .
.
(2)由(1)不妨設(shè)M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,

![]() ,
,
當(dāng)![]() 時,
時, ![]() ,
,
所以△MON面積的最大值為![]() .
.
【題型】解答題
【結(jié)束】
23
【題目】已知函數(shù)![]() 的定義域為
的定義域為![]() ;
;
(1)求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)實數(shù)![]() 為
為![]() 的最大值,若實數(shù)
的最大值,若實數(shù)![]() ,
, ![]() ,
, ![]() 滿足
滿足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】上饒某購物中心在開業(yè)之后,為了解消費者購物金額的分布,在當(dāng)月的電腦消費小票中隨機抽取![]() 張進行統(tǒng)計,將結(jié)果分成5組,分別是
張進行統(tǒng)計,將結(jié)果分成5組,分別是![]() ,制成如圖所示的頻率分布直方圖(假設(shè)消費金額均在
,制成如圖所示的頻率分布直方圖(假設(shè)消費金額均在![]() 元的區(qū)間內(nèi)).
元的區(qū)間內(nèi)).

(1)若在消費金額為![]() 元區(qū)間內(nèi)按分層抽樣抽取6張電腦小票,再從中任選2張,求這2張小票均來自
元區(qū)間內(nèi)按分層抽樣抽取6張電腦小票,再從中任選2張,求這2張小票均來自![]() 元區(qū)間的概率;
元區(qū)間的概率;
(2)為做好五一勞動節(jié)期間的商場促銷活動,策劃人員設(shè)計了兩種不同的促銷方案:
方案一:全場商品打8.5折;
方案二:全場購物滿200元減20元,滿400元減50元,滿600元減80元,滿800元減120元,以上減免只取最高優(yōu)惠,不重復(fù)減免.利用直方圖的信息分析哪種方案優(yōu)惠力度更大,并說明理由(直方圖中每個小組取中間值作為該組數(shù)據(jù)的替代值).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 為橢圓
為橢圓![]() 上任一點,
上任一點, ![]() 為其右焦點,點
為其右焦點,點![]() 滿足
滿足![]() .
.
①證明: ![]() 為定值;
為定值;
②設(shè)直線![]() 與橢圓
與橢圓![]() 有兩個不同的交點
有兩個不同的交點![]() ,與
,與![]() 軸交于點
軸交于點![]() .若
.若![]() 成等差數(shù)列,求
成等差數(shù)列,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com