
【題目】(本小題滿分12分)
如圖,在五棱錐![]() 中,
中,![]() ,且
,且![]() .
.
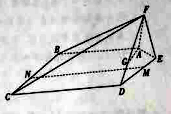
(1)已知點![]() 在線段
在線段![]() 上,確定
上,確定![]() 的位置,使得
的位置,使得![]() ;
;
(2)點![]() 分別在線段
分別在線段![]() 上,若沿直線
上,若沿直線![]() 將四邊形
將四邊形![]() 向上翻折,
向上翻折,![]() 與
與![]() 恰好重合,求直線
恰好重合,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)點![]() 為靠近
為靠近![]() 的三等分點;(2)
的三等分點;(2)![]() .
.
【解析】
試題分析:(1)當點![]() 為靠近
為靠近![]() 的三等分點時,在線段
的三等分點時,在線段![]() 取一點
取一點![]() ,使得
,使得![]() ,連結
,連結![]() ,可證四邊形
,可證四邊形![]() 為平行四邊形,得
為平行四邊形,得![]() ,再根據比例關系得
,再根據比例關系得![]() ,從而得平面
,從而得平面![]() 平面
平面![]() ,進而得結論;(2)如圖,建立空間直角坐標系
,進而得結論;(2)如圖,建立空間直角坐標系![]() ,可得
,可得![]() ,再列方程組求出平面
,再列方程組求出平面![]() 的一個法向量,根據空間向量夾角余弦公式求解即可.
的一個法向量,根據空間向量夾角余弦公式求解即可.
試題解析:(1)點![]() 為靠近
為靠近![]() 的三等分點.
的三等分點.
在線段![]() 取一點
取一點![]() ,使得
,使得![]() ,連結
,連結![]() .
.
![]() .
.
又![]() ,
,![]() 四邊形
四邊形![]() 為平行四邊形,
為平行四邊形,![]() .
.
![]() 點
點![]() 為靠近
為靠近![]() 的三等分點,
的三等分點,![]() .
.
![]() ,而
,而![]() .
.
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,又
,又![]() ,
,
![]() .
.
如圖,建立空間直角坐標系![]() ,則
,則 .
.
設![]() .則
.則![]()
![]() 翻折后,
翻折后,![]() 與
與![]() 重合,
重合,![]() ,又
,又![]() .
.
故![]() ,從而,
,從而,![]() .
.
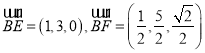 .
.

設![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
則
取![]() ,則
,則![]() .
.
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,則
,則 ,
,
故直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程為
的參數方程為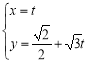 (
(![]() 為參數),若以直角坐標系
為參數),若以直角坐標系![]() 的
的![]() 點為極點,
點為極點,![]() 方向為極軸,選擇相同的長度單位建立極坐標系,得曲線
方向為極軸,選擇相同的長度單位建立極坐標系,得曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的傾斜角和曲線
的傾斜角和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,設點
兩點,設點![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】漳州市博物館為了保護一件珍貴文物,需要在館內一種透明又密封的長方體玻璃保護罩內充入保護液體.該博物館需要支付的總費用由兩部分組成:①罩內該種液體的體積比保護罩的容積少0.5立方米,且每立方米液體費用500元;②需支付一定的保險費用,且支付的保險費用與保護罩容積成反比,當容積為2立方米時,支付的保險費用為4000元.
(Ⅰ)求該博物館支付總費用![]() 與保護罩容積
與保護罩容積![]() 之間的函數關系式;
之間的函數關系式;
(Ⅱ)求該博物館支付總費用的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
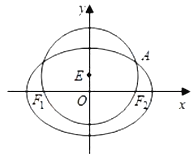
【題目】已知圓![]() :
: ![]() 經過橢圓
經過橢圓![]() :
: ![]() 的左右焦點
的左右焦點![]() ,且與橢圓
,且與橢圓![]() 在第一象限的交點為
在第一象限的交點為![]() ,且
,且![]() 三點共線,直線
三點共線,直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,且
兩點,且![]() (
(![]() ).
).
(1)求橢圓![]() 的方程;
的方程;
(2)當三角形![]() 的面積取得最大值時,求直線
的面積取得最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題錯誤的是 ( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 內一定存在直線平行于平面
內一定存在直線平行于平面![]()
B. 如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 內一定不存在直線垂直于平面
內一定不存在直線垂直于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,那么
,那么![]()
D. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 內所有直線都垂直于平面
內所有直線都垂直于平面![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com