
(1)設(shè)4<t<4![]() ,求向量
,求向量![]() 與
與![]() 的夾角θ的取值范圍;
的夾角θ的取值范圍;
(2)設(shè)以原點O為中心,對稱軸在坐標(biāo)軸上,以F為右焦點的橢圓經(jīng)過點M,且|![]() |=c,t=(
|=c,t=(![]() -1)c2,當(dāng)|
-1)c2,當(dāng)|![]() |取最小值時,求橢圓的方程.
|取最小值時,求橢圓的方程.
思路解析:此題是向量知識與圓錐曲線結(jié)合的一個問題,高考試題常用向量給出條件,運用向量知識進行轉(zhuǎn)化為圓錐曲線的有關(guān)問題是常考的思想方法.設(shè)求向量![]() 與
與![]() 的夾角θ的取值范圍由面積公式及
的夾角θ的取值范圍由面積公式及![]() ·
·![]() =t,可求出tanθ的范圍.(2)中設(shè)出P點的坐標(biāo),用c來表示|
=t,可求出tanθ的范圍.(2)中設(shè)出P點的坐標(biāo),用c來表示|![]() |,求出當(dāng)c取某值時的|
|,求出當(dāng)c取某值時的|![]() |的最小值,進而求橢圓的方程.
|的最小值,進而求橢圓的方程.
解:(1)由2![]() =
=![]() |
|![]() |·|
|·|![]() |·sinθ,得?|
|·sinθ,得?|![]() |·|
|·|![]() |=
|=![]() ,
,
由cosθ=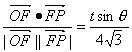 ,得tanθ=
,得tanθ=![]() .
.
∵4<t<4![]() ,∴1<tanθ<
,∴1<tanθ<![]() .
.
∵θ∈[0,π],∴夾角θ的取值范圍是(![]() ,
,![]() ).
).
(2)設(shè)P(x0,y0),則![]() =(x0-c,y0),
=(x0-c,y0),![]() =(c,0).
=(c,0).
∴![]() ·
·![]() =(x0-c,y0)·(c,0)=(x0-c)c=t=(
=(x0-c,y0)·(c,0)=(x0-c)c=t=(![]() -1)c2.
-1)c2.
∴x0=![]() c.
c.
S△OFP=![]() |
|![]() |·|y0|=2
|·|y0|=2![]() ,
,
∴y0=±![]() .
.
又由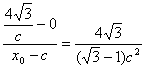 ,
,
得x0=![]() c.
c.
∴|![]() |=
|=![]() .
.
∴當(dāng)且僅當(dāng)![]() c=
c=![]() ,即c=2時,?|
,即c=2時,?|![]() |取最小值2
|取最小值2![]() ,
,
此時, ![]() =(2
=(2![]() ,±2
,±2![]() ),
),
∴![]() =
=![]() (2
(2![]() ,2
,2![]() )+(0,1)=(2,3)或
)+(0,1)=(2,3)或![]() =
=![]() (2
(2![]() ,-2
,-2![]() )+(0,1)=(2,-1).
)+(0,1)=(2,-1).
橢圓長軸2a=![]() =8,
=8,
∴a=4,b2=12或2a=![]() .
.
∴a=![]() ,b2=
,b2=![]() .
.
故所求橢圓方程為![]() =1或
=1或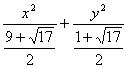 =1.
=1.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
|
| π |
| 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
|
| π |
| 6 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
|
| OM |
| OC |
| A、-1 | B、0 | C、3 | D、4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 3 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com