【題目】近年來我國電子商務行業迎來發展的新機遇，與此同時，相關管理部門推出了針對電商商品和服務的評價體系．現從評價系統中選出200次成功交易，并對其評價進行統計，對商品好評率為
，對服務好評率為
，其中對商品和服務都做出好評的交易為80次．
（1）是否可以在犯錯誤率不超過0.1%的前提下，認為商品好評與服務好評有關？
（2）若針對商品的好評率，采用分層抽樣的方式從這200次交易中取出5次交易，并從中選擇兩次交易進行客戶回訪，求只有一次好評的概率．
注：1.
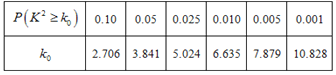
注2. 
【答案】（1）見解析；（2）
.
【解析】試題分析：（1）由已知列出關于商品和服務評價的2×2列聯表，代入公式求得k2的值，對應數表得答案；
（2）采用分層抽樣的方式從這200次交易中取出5次交易，則好評的交易次數為3次，不滿意的次數為2次，利用枚舉法得到從5次交易中，取出2次的所有取法，查出其中只有一次好評的情況數，然后利用古典概型概率計算公式求得只有一次好評的概率．
試題解析：
（1）由題意可得關于商品評價和服務評價的
列聯表：
對服務好評 | 對服務不滿意 | 合計 | |
對商品好評 | 80 | 40 | 120 |
對商品不滿意 | 70 | 10 | 80 |
合計 | 150 | 50 | 200 |
所以
，
所以可以在犯錯誤概率不超過0.1%的前提下，認為商品好評與服務好評有關．
（2）若針對商品的好評率，采用分層抽樣的方式從這200次交易中取出5次交易，則好評的交易次數為3次，不滿意的次數為2次，令好評的交易為
，不滿意的交易為
.
從5次交易中，取出2次的所有取法
．共計10種情況．
其中只有一次好評的情況是
，共計6種情況．
因此，只有一次好評的概率為
．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知A，B，C為銳角△ABC的內角， 
=（sinA，sinBsinC）， 
=（1，﹣2）， ⊥ ．
（1）tanB，tanBtanC，tanC能否構成等差數列？并證明你的結論；
（2）求tanAtanBtanC的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一次購物抽獎活動中，假設某10張券中有一等獎券1張，可獲價值50元的獎品；有二等獎券3張，每張可獲價值10元的獎品；其余6張沒有獎，某顧客從此10張券中任抽2張，求：
（Ⅰ）該顧客中獎的概率；
（Ⅱ）該顧客獲得的獎品總價值ξ（元）的概率分布列和期望Eξ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
，又
是一個常數，已知
或
時， 
只有一個實根，當
時， 
有三個相異實根，給出下列命題：
①
和
有一個相同的實根；
②
和
有一個相同的實根；
③
的任一實根大于
的任一實根；
④
的任一實根小于
的任一實根．
其中正確命題的個數為（ ）
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1=1，an+1+an= 
﹣ 
，n∈N* ．
（Ⅰ）求a2 ， a3 ， a4；
（Ⅱ）猜想數列{an}的通項公式，并用數學歸納法證明．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，以
為極點，
軸正半軸為極軸建立極坐標系，圓
的極坐標方程為
，直線
的參數方程為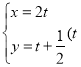
為參數），直線和圓交于
兩點，
是圓上不同于的任意一點．
（1）求圓心的極坐標；
（2）求點到直線的距離的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以平面直角坐標系
的原點為極點， 
軸正半軸為極軸且取相同的單位長度建立極坐標系．已知點
的參數方程為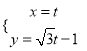
（
為參數），點
在曲線
上．
（1）求在平面直角坐標系
中點
的軌跡方程和曲線
的普通方程；
（2）求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=lnx﹣ax+ 
﹣1． （Ⅰ）當a=1時，求曲線f（x）在x=1處的切線方程；
（Ⅱ）當a= 
時，求函數f（x）的單調區間；
（Ⅲ）在（Ⅱ）的條件下，設函數g（x）=x2﹣2bx﹣ 
，若對于x1∈[1，2]，x2∈[0，1]，使f（x1）≥g（x2）成立，求實數b的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
