已知函數f(x)=x2+ax+b2,分別在下列條件下求不等式f(x)>0的解集為R的概率.
(1)a,b∈Z,且-2≤a≤4,-2≤b≤4;
(2)若a,b∈R,且0<a≤2,0<b≤2.
【答案】
分析:(1)本小題是一個等可能事件的概率,試驗發生包含的事件是從兩個集合中各取一個數字,共有49種結果,滿足條件的事件是不等式f(x)>0的解集為R,即a
2<4b
2,列舉出所有的事件數,根據等可能事件的概率得到結果.
(2)本題是一個等可能事件的概率,試驗發生包含的事件是在區間(0,2]上任取兩個數a和b,寫出事件對應的集合,做出面積,滿足條件的事件是求不等式f(x)>0的解集為R,根據二次方程的判別式寫出a,b要滿足的條件,寫出對應的集合,做出面積,得到概率.
解答:解:(1)由題意知本題是一個等可能事件的概率,
試驗發生包含的事件是從兩個集合中各取一個數字,共有49種結果,
滿足條件的事件是求不等式f(x)>0的解集為R,
即a
2<4b
2,
當b=-2,2,3,4時,a有7種;
當b=-1,1時,a有5種;
當b=0時,a有1種;
共有39種結果,
∴所求的概率是
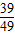
(2)由題意知本題是一個等可能事件的概率,
∵試驗發生包含的事件是在區間[0,2]上任取兩個數a和b,
事件對應的集合是Ω={(a,b)|0≤a≤2,0≤b≤2}
對應的面積是s
Ω=4
滿足條件的事件是關于x的不等式f(x)>0的解集為R,
即a
2-4b
2≤0,
∴a≤2b,
事件對應的集合是A={(a,b)|0≤a≤2,0≤b≤2,a≤2b}
對應的圖形的面積是s
A=3
∴根據等可能事件的概率得到P=

故答案為:

.
點評:本題考查等可能事件的概率,考查一元二次方程的解,考查列舉法的應用,是一個綜合題目,本題解題的關鍵是弄清楚一元二次方程解的情況.本題考查幾何概型,古典概型和幾何概型是我們學習的兩大概型,古典概型要求能夠列舉出所有事件和發生事件的個數,而不能列舉的就是幾何概型,幾何概型的概率的值是通過長度、面積、和體積、的比值得到.

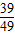

 .
.

 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<