
【題目】已知函數f(x)=ax2+x﹣lnx,(a>0). (Ⅰ)求f(x)的單調區間;
(Ⅱ)設f(x)極值點為x0 , 若存在x1 , x2∈(0,+∞),且x1≠x2 , 使f(x1)=f(x2),求證:x1+x2>2x0 .
【答案】解:( I)f(x)定義域為(0,+∞), f′(x)= ![]() ,
,
∵a>0,∴方程f′(x)=0有兩個實根x1= ![]() <0,x2=
<0,x2= ![]() >0,
>0,
當x∈(0,x2)時,f′(x)<0,當x∈(x2 , +∞)時,f′(x)>0,
∴f(x)的單調增區間為:( ![]() ,+∞)減區間為(0,
,+∞)減區間為(0, ![]() )
)
( II)要證x1+x2>2x0 , 需證 ![]() .
.
由( I)知, ![]() ,f′(x)=2ax+1﹣
,f′(x)=2ax+1﹣ ![]() 在(0,+∞)上單調遞增,
在(0,+∞)上單調遞增,
∴只需證f′( ![]() )>0
)>0
不妨設x2>x1>0
由已知得 ![]() =
= ![]() ,=[a(x2+x1)+1](x2﹣x1)﹣(lnx2﹣lnx1)=0
,=[a(x2+x1)+1](x2﹣x1)﹣(lnx2﹣lnx1)=0
∴ ![]()
∵ ![]()
∴ ![]()
法1: ![]() =
= ![]()
令 ![]()
∴ 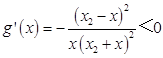 ,∴g(x)在(0,x2)單調遞減,
,∴g(x)在(0,x2)單調遞減,
∴g(x1)>g(x2)=0,
又 ![]() ,∴
,∴ ![]() 成立.∴結論成立.
成立.∴結論成立.
法2:f′( ![]() )=
)= 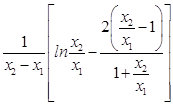 .
.
設 ![]() ,
, ![]() .∵
.∵ 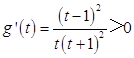 ,
,
∴g(t)在(1,+∞)上是增函數,∴g(t)>g(1)=0,
即 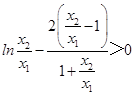 ,
,
又∵ ![]() ,∴f′(
,∴f′( ![]() )>0成立.
)>0成立.
∴結論成立
【解析】(Ⅰ)先求出函數的定義域,求出函數f(x)的導函數,在定義域下令導函數大于0得到函數的遞增區間.即可求出單調減區間.(Ⅱ)要證x1+x2>2x0 , 需證 ![]() .由( I)知,
.由( I)知, ![]() ,f′(x)=2ax+1﹣
,f′(x)=2ax+1﹣ ![]() 在(0,+∞)上單調遞增,只需證f′(
在(0,+∞)上單調遞增,只需證f′( ![]() )>0.
)>0.
【考點精析】掌握利用導數研究函數的單調性和函數的極值與導數是解答本題的根本,需要知道一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值.
是極小值.


科目:高中數學 來源: 題型:
【題目】如圖,四面體ABCD中,△ABC是以BC為斜邊的等腰直角三角形,△BCD是邊長為2的正三角形.

(Ⅰ)當AD為多長時,![]() ?
?
(Ⅱ)當二面角B﹣AC﹣D為![]() 時,求AD的長.
時,求AD的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖.
分組的頻率分布直方圖如圖.

(1)求直方圖中![]() 的值;
的值;
(2)求月平均用電量的平均數、眾數和中位數;
(3)在月平均用電量為,![]() ,
,![]() ,
,![]() ,
,![]() 的四組用戶中,用分層抽樣的方法抽取11戶居民,則月平均用電量在
的四組用戶中,用分層抽樣的方法抽取11戶居民,則月平均用電量在![]() 的用戶中應抽取多少戶?
的用戶中應抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費用支出![]() 與銷售額
與銷售額![]() 之間有如下的對應數據(單位:萬元):
之間有如下的對應數據(單位:萬元):
![]()
(1)求![]() 關于
關于![]() 的線性回歸直線方程;
的線性回歸直線方程;
(2)據此估計廣告費用為10萬元時銷售收入![]() 的值.
的值.
(附:對于線性回歸方程![]() ,其中
,其中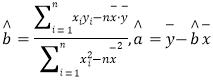 )
)
參考公式: 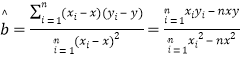
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《九章算術》中“開立圓術”曰:置積尺數,以十六乘之,九而一,所得開立方除之,即立圓徑,“開立圓術”相當于給出了已知球的體積V,求其直徑d的一個近似公式d≈ ![]() .人們還用過一些類似的近似公式.根據π=3.14159…..判斷,下列近似公式中最精確的一個是( )
.人們還用過一些類似的近似公式.根據π=3.14159…..判斷,下列近似公式中最精確的一個是( )
A.d≈ ![]()
B.d≈ ![]()
C.d≈ ![]()
D.d≈ ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形ACDE所在的平面與平面ABC垂直,M是CE和AD的交點,AC![]() BC,且AC=BC.
BC,且AC=BC.
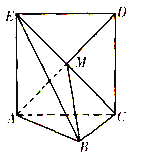
(1)求證:AM![]() 平面EBC;
平面EBC;
(2)求直線AB與平面EBC所成角的大小,
(3)求二面角A-BE-C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了政府對過熱的房地產市場進行調控決策,統計部門對城市人和農村人進行了買房心理預測調研,用簡單隨機抽樣的方法抽取了110人進行統計,得到如下列聯表:
買房 | 不買房 | 糾結 | |
城市人 | 5 | 15 | |
農村人 | 20 | 10 |
已知樣本中城市人數與農村人數之比是3:8.
(Ⅰ)分別求樣本中城市人中的不買房人數和農村人中的糾結人數;
(Ⅱ)從參與調研的城市人中用分層抽樣方法抽取6人,進一步統計城市人的某項收入指標,假設一個買房人的指標算作3,一個糾結人的指標算作2,一個不買房人的指標算作1,現在從這6人中再隨機選取3人,令X=再抽取3人指標之和,求X的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com