
【題目】已知⊙O:x2+y2=1和定點A(2,1),由⊙O外一點P(a,b)向⊙O引切線PQ,切點為Q,且滿足|PQ|=|PA|.
(1)求實數a,b間滿足的等量關系;
(2)求線段PQ長的最小值;
(3)若以P為圓心所作的⊙P與⊙O有公共點,試求半徑最小值時⊙P的方程.
【答案】
(1)解:連接OQ,∵切點為Q,PQ⊥OQ,由勾股定理可得 PQ2=OP2﹣OQ2.
由已知PQ=PA,可得 PQ2=PA2,即 (a2+b2)﹣1=(a﹣2)2+(b﹣1)2.
化簡可得 2a+b﹣3=0
(2)解:
∵PQ= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
故當a= ![]() 時,線段PQ取得最小值為
時,線段PQ取得最小值為 ![]()
(3)解:若以P為圓心所作的⊙P 的半徑為R,由于⊙O的半徑為1,∴|R﹣1|≤PO≤R+1.
而OP= ![]() =
= ![]() =
= ![]() ,故當a=
,故當a= ![]() 時,PO取得最小值為
時,PO取得最小值為 ![]() ,
,
此時,b=﹣2a+3= ![]() ,R取得最小值為
,R取得最小值為 ![]() ﹣1.
﹣1.
故半徑最小時⊙P 的方程為 ![]() +
+ ![]() =
= ![]()
【解析】(1)由勾股定理可得 PQ2=OP2﹣OQ2=PA2 , 即 (a2+b2)﹣1=(a﹣2)2+(b﹣1)2 , 化簡可得a,b間滿足的等量關系.(2)由于 PQ= ![]() =
= ![]() ,利用二次函數的性質求出它的最小值.(3)設⊙P 的半徑為R,可得|R﹣1|≤PO≤R+1.利用二次函數的性質求得OP=
,利用二次函數的性質求出它的最小值.(3)設⊙P 的半徑為R,可得|R﹣1|≤PO≤R+1.利用二次函數的性質求得OP= ![]() 的最小值為
的最小值為 ![]() ,此時,求得b=﹣2a+3=
,此時,求得b=﹣2a+3= ![]() ,R取得最小值為
,R取得最小值為 ![]() ﹣1,從而得到圓的標準方程.
﹣1,從而得到圓的標準方程.


科目:高中數學 來源: 題型:
【題目】已知A(0,1)、B(0,2)、C(4t,2t2﹣1)(t∈R),⊙M是以AC為直徑的圓,再以M為圓心、BM為半徑作圓交x軸交于D、E兩點.
(Ⅰ)若△CDE的面積為14,求此時⊙M的方程;
(Ⅱ)試問:是否存在一條平行于x軸的定直線與⊙M相切?若存在,求出此直線的方程;若不存在,請說明理由;
(Ⅲ)求 ![]() 的最大值,并求此時∠DBE的大小.
的最大值,并求此時∠DBE的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年高一新生入學后,為了了解新生學業水平,某區對新生進行了水平測試,隨機抽取了50名新生的成績,其相關數據統計如下:
分數段 | 頻數 | 選擇題得分24分以上(含24分) |
| 5 | 2 |
| 10 | 4 |
| 15 | 12 |
| 10 | 6 |
| 5 | 4 |
| 5 | 5 |
(Ⅰ)若從分數在![]() ,
, ![]() 的被調查的新生中各隨機選取2人進行追蹤調查,求恰好有2名新生選擇題得分不足24分的概率;
的被調查的新生中各隨機選取2人進行追蹤調查,求恰好有2名新生選擇題得分不足24分的概率;
(Ⅱ)在(Ⅰ)的條件下,記選中的4名新生中選擇題得分不足24分的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三角形ABC的頂點坐標為A(﹣1,5)、B(﹣2,﹣1)、C(4,3).
(1)求AB邊上的高線所在的直線方程;
(2)求三角形ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
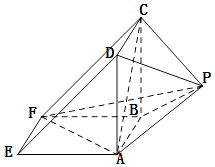
【題目】如圖所示,該幾何體是由一個直三棱柱ADE﹣BCF和一個正四棱錐P﹣ABCD組合而成,AD⊥AF,AE=AD=2.
(Ⅰ)證明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱錐P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2x+t,g(x)=x2﹣t(t∈R)
(1)當x∈[2,3]時,求函數f(x)的值域(用t表示)
(2)設集合A={y|y=f(x),x∈[2,3]},B={y|y=|g(x)|,x∈[2,3]},是否存在正整數t,使得A∩B=A.若存在,請求出所有可能的t的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市規定,高中學生在校期間須參加不少于80小時的社區服務才合格.某校隨機抽取20位學生參加社區服務的數據,按時間段[75,80),[80,85),[85,90),[90,95),[95,100](單位:小時)進行統計,其頻率分布直方圖如圖所示. 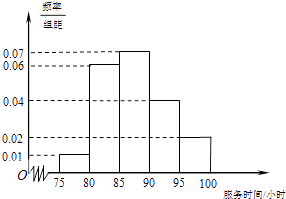
(1)求抽取的20人中,參加社區服務時間不少于90小時的學生人數;
(2)從參加社區服務時間不少于90小時的學生中任意選取2人,求所選學生的參加社區服務時間在同一時間段內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某景區修建一棟復古建筑,其窗戶設計如圖所示.圓![]() 的圓心與矩形
的圓心與矩形![]() 對角線的交點重合,且圓與矩形上下兩邊相切(
對角線的交點重合,且圓與矩形上下兩邊相切(![]() 為上切點),與左右兩邊相交(
為上切點),與左右兩邊相交(![]() ,
, ![]() 為其中兩個交點),圖中陰影部分為不透光區域,其余部分為透光區域.已知圓的半徑為1m,且
為其中兩個交點),圖中陰影部分為不透光區域,其余部分為透光區域.已知圓的半徑為1m,且![]() .設
.設![]() ,透光區域的面積為
,透光區域的面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數關系式,并求出定義域;
的函數關系式,并求出定義域;
(2)根據設計要求,透光區域與矩形窗面的面積比值越大越好.當該比值最大時,求邊![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cosxsin(x+ ![]() )﹣
)﹣ ![]() .
.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)△ABC中,角A,B,C所對的邊為a,b,c,f( ![]() )=
)= ![]() ,B=
,B= ![]() ,a=1,求△ABC的面積.
,a=1,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com